题目内容
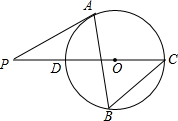 如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.(1)求∠ACP的度数;
(2)求证:PA是⊙O的切线.
考点:切线的判定
专题:
分析:(1)连接OA,根据圆周角定理求出∠AOC,再由OA=OC得出∠ACO=∠OAC=30°,从而求得∠ACP的度数;
(2)由AP=AC得出∠P=30°,继而由∠OAP=∠AOC-∠P,可得出OA⊥PA,从而得出结论;
(2)由AP=AC得出∠P=30°,继而由∠OAP=∠AOC-∠P,可得出OA⊥PA,从而得出结论;
解答:(1)解:连接OA,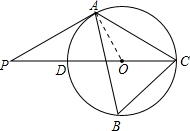
∵∠B=60°,
∴∠AOC=2∠B=120°,
又∵OA=OC,
∴∠OAC=∠OCA=30°,
即∠ACP=30°.
(2)证明∵AP=AC,
∴∠ACP=∠P=30°,
∴∠OAP=∠AOC-∠P=90°,
∴OA⊥PA,
∴PA是⊙O的切线.

∵∠B=60°,
∴∠AOC=2∠B=120°,
又∵OA=OC,
∴∠OAC=∠OCA=30°,
即∠ACP=30°.
(2)证明∵AP=AC,
∴∠ACP=∠P=30°,
∴∠OAP=∠AOC-∠P=90°,
∴OA⊥PA,
∴PA是⊙O的切线.
点评:本题考查了切线的判定及圆周角定理,解答本题的关键是掌握切线的判定定理、圆周角定理及含30°直角三角形的性质.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
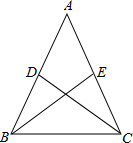 如图,在△ABC中,AB=AC,D、E分别是AB、AC上的点,要使△ABE≌△ACD,应补充条件( )
如图,在△ABC中,AB=AC,D、E分别是AB、AC上的点,要使△ABE≌△ACD,应补充条件( )| A、∠A=∠A |
| B、BE=CD |
| C、∠ABE=∠ACD |
| D、∠ABC=∠ACB. |
 如图所示,AB∥EF∥CD,∠ABC=90°,AB=DC,那么图中的全等三角形有( )
如图所示,AB∥EF∥CD,∠ABC=90°,AB=DC,那么图中的全等三角形有( )| A、4对 | B、3对 | C、2对 | D、1对 |
在数轴上与-3的距离是15的点表示的数是( )
| A、18 | B、±18 |
| C、12或-18 | D、-12或18 |
 如图,△ABC中,AB=13,BC=14,AC=15.点P从点B出发,以每秒2个单位的速度沿射线BC运动.设点P运动的时间为t秒,求当t为何值时,△ABP为等腰三角形?
如图,△ABC中,AB=13,BC=14,AC=15.点P从点B出发,以每秒2个单位的速度沿射线BC运动.设点P运动的时间为t秒,求当t为何值时,△ABP为等腰三角形? 如图,O为直线AB上一点,∠AOC=58°,OD平分∠AOC,∠DOE=90°.
如图,O为直线AB上一点,∠AOC=58°,OD平分∠AOC,∠DOE=90°.