题目内容
若抛物线y=x2-mx+2m-1与x轴两交点的横坐标为x1、x2,且x12+x22=7,则(x1-x2)2的值为 .
考点:抛物线与x轴的交点
专题:
分析:根据根与系数的关系得到x1+x2=m,x1x2=2m-1,由x12+x22=7变形得(x1+x2)2-2x1x2=7,则m2-2(2m-1)=7,解得m1=5,m2=-1,再根据判别式的意义确定m=-1,则x1+x2=-1,x1x2=-3,然后根据完全平方公式得到(x1-x2)2=(x1+x2)2-4x1x2,再利用整体代入的方法计算.
解答:解:根据题意得x1+x2=m,x1x2=2m-1,
∵x12+x22=7,
∴(x1+x2)2-2x1x2=7,
∴m2-2(2m-1)=7,
整理得m2-4m-5=0,解得m1=5,m2=-1,
当m=5时,原方程变形为x2-5m+9=0,△=25-4×9<0,此方程没有实数解,故舍去,
∴m=-1,
∴x1+x2=-1,x1x2=-3,
∴(x1-x2)2=(x1+x2)2-4x1x2=1+12=13.
故答案为:13.
∵x12+x22=7,
∴(x1+x2)2-2x1x2=7,
∴m2-2(2m-1)=7,
整理得m2-4m-5=0,解得m1=5,m2=-1,
当m=5时,原方程变形为x2-5m+9=0,△=25-4×9<0,此方程没有实数解,故舍去,
∴m=-1,
∴x1+x2=-1,x1x2=-3,
∴(x1-x2)2=(x1+x2)2-4x1x2=1+12=13.
故答案为:13.
点评:本题考查了抛物线与x轴交点问题,求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
在数轴上与-3的距离是15的点表示的数是( )
| A、18 | B、±18 |
| C、12或-18 | D、-12或18 |
 如图所示,已知∠1=∠2,AC平分∠DAB,试说明DC∥AB.
如图所示,已知∠1=∠2,AC平分∠DAB,试说明DC∥AB.
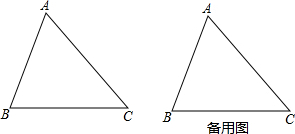 如图,△ABC中,AB=13,BC=14,AC=15.点P从点B出发,以每秒2个单位的速度沿射线BC运动.设点P运动的时间为t秒,求当t为何值时,△ABP为等腰三角形?
如图,△ABC中,AB=13,BC=14,AC=15.点P从点B出发,以每秒2个单位的速度沿射线BC运动.设点P运动的时间为t秒,求当t为何值时,△ABP为等腰三角形?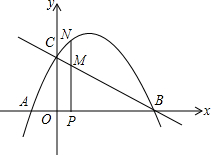 如图,抛物线
如图,抛物线 如图,在平面直角坐标系中,点O为坐标原点,等腰△ABC,CA=CB,点A在x轴负半轴上,点B在x轴正半轴上,点C在y轴正半轴上,AB=OC,△ABC的面积为32,点D为AC中点,过点D作x轴的平行线交y轴于点E.
如图,在平面直角坐标系中,点O为坐标原点,等腰△ABC,CA=CB,点A在x轴负半轴上,点B在x轴正半轴上,点C在y轴正半轴上,AB=OC,△ABC的面积为32,点D为AC中点,过点D作x轴的平行线交y轴于点E.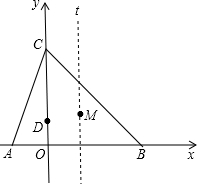 如图,平面直线坐标中,A(-1,0),点C为y轴正半轴上一点,且AC=
如图,平面直线坐标中,A(-1,0),点C为y轴正半轴上一点,且AC=