题目内容
10. 如图,两条相交线段上有9个点,一共可以组成60个不同的三角形.
如图,两条相交线段上有9个点,一共可以组成60个不同的三角形.
分析 直线b上有6个点,可以与点A7组成6×(6-1)÷2=15个三角形,同理,可以与点A8组成6×(6-1)÷2=15个三角形,与点A9组成6×(6-1)÷2=15个三角形.
直线a上有3个点,可以与点A1组成3×(3-1)÷2=3个三角形,则易求直线a上3个点与直线b上的点所组成的三角形的个数.
解答  解:①直线直线b上有6个点,可以与点A7组成三角形的个数是:6×(6-1)÷2=15(个).
解:①直线直线b上有6个点,可以与点A7组成三角形的个数是:6×(6-1)÷2=15(个).
同理,可以与点A8组成三角形的个数是:6×(6-1)÷2=15(个).
与点A9组成三角形的个数是:6×(6-1)÷2=15(个).
②直线a上有3个点,可以与点A1组成三角形的个数是:3×(3-1)÷2=3(个).
同理,可以与点A2组成三角形的个数是:3×(3-1)÷2=3(个).
可以与点A3组成三角形的个数是:3×(3-1)÷2=3(个).
可以与点A5组成三角形的个数是:3×(3-1)÷2=3(个).
可以与点A6组成三角形的个数是:3×(3-1)÷2=3(个).
则总的三角形的个数是:15×3+3×15=60(个).
故答案是:60.
点评 本题考查了三角形.数三角形的个数,可以按照数线段条数的方法,如果一条线段上有n个点,那么就有$\frac{n(n-1)}{2}$条线段,也可以与线段外的一点组成$\frac{n(n-1)}{2}$个三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20. 四个规模不同的滑梯A,B,C,D,它们的滑板长(平直的)分别为300m,250m,200m,200m;滑板与地面所成的角度分别为30°,45°,45°,60°,则关于四个滑梯的高度正确说法( )
四个规模不同的滑梯A,B,C,D,它们的滑板长(平直的)分别为300m,250m,200m,200m;滑板与地面所成的角度分别为30°,45°,45°,60°,则关于四个滑梯的高度正确说法( )
 四个规模不同的滑梯A,B,C,D,它们的滑板长(平直的)分别为300m,250m,200m,200m;滑板与地面所成的角度分别为30°,45°,45°,60°,则关于四个滑梯的高度正确说法( )
四个规模不同的滑梯A,B,C,D,它们的滑板长(平直的)分别为300m,250m,200m,200m;滑板与地面所成的角度分别为30°,45°,45°,60°,则关于四个滑梯的高度正确说法( )| A. | A的最高 | B. | B的最高 | C. | C的最高 | D. | D的最高 |
1. 如图,PA、PB是⊙O的切线,AC是⊙O的直径,∠P=62°,则∠BOC的度数为( )
如图,PA、PB是⊙O的切线,AC是⊙O的直径,∠P=62°,则∠BOC的度数为( )
 如图,PA、PB是⊙O的切线,AC是⊙O的直径,∠P=62°,则∠BOC的度数为( )
如图,PA、PB是⊙O的切线,AC是⊙O的直径,∠P=62°,则∠BOC的度数为( )| A. | 60° | B. | 62° | C. | 31° | D. | 70° |
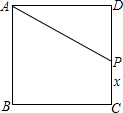 如图.正方形ABCD的边长为4cm.P为DC上的点,当点P从C向D移动时,四边形APCB的面积发生了变化.
如图.正方形ABCD的边长为4cm.P为DC上的点,当点P从C向D移动时,四边形APCB的面积发生了变化.
 如图,已知△ABC中,∠A=60°,D为AB上一点,且AC=2AD+BD,∠B=4∠ACD,则∠DCB的度数是20°.
如图,已知△ABC中,∠A=60°,D为AB上一点,且AC=2AD+BD,∠B=4∠ACD,则∠DCB的度数是20°.