题目内容
10. 如图,已知△ABC中,∠A=60°,D为AB上一点,且AC=2AD+BD,∠B=4∠ACD,则∠DCB的度数是20°.
如图,已知△ABC中,∠A=60°,D为AB上一点,且AC=2AD+BD,∠B=4∠ACD,则∠DCB的度数是20°.
分析 通过作辅助线构造等边三角形,利用等边三角形的性质,得到角相等,边相等,根据三角形全等,得到角相等,利用外角的性质列方程求解.
解答 解: 如图延长AB到E使BE=AD,连接CE,
如图延长AB到E使BE=AD,连接CE,
∴AE=AD+DB+BE=2AD+BD,
∵AC=2AD+BD,
∴AE=AC,∵∠A=60°,
∴△AEC是等边三角形,
∴∠E=∠ACE=60°,
∵∠B=4∠ACD,
设∠ACD=x,则∠ABC=4x,
在△ADC与△EBC中,$\left\{\begin{array}{l}{AD=BE}\\{∠A=∠E}\\{AC=EC}\end{array}\right.$,
∴△ADC≌△EBC,
∠ACD=∠ECB=x,
∴∠ABC=∠E+∠BCE,
∴4x=60°+x,∴x=20°,
∴∠BCD=60°-20°-20°=20°,
故答案为:20°
点评 本题主要考查了等边三角形的判定和性质,全等三角形的判定和性质,外交的性质,列方程求解等知识点.

练习册系列答案
相关题目
19.如图,∠1和∠2是同位角的有( )
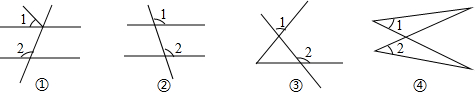
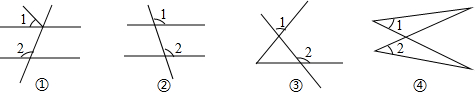
| A. | ①② | B. | ①③ | C. | ②③ | D. | ②④ |
 如图,两条相交线段上有9个点,一共可以组成60个不同的三角形.
如图,两条相交线段上有9个点,一共可以组成60个不同的三角形.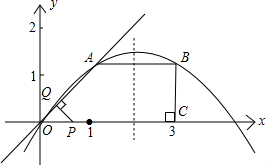 如图所示,已知在直角梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,1)、B(3,1).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ垂直于直线OA,垂足为Q.设P点移动的时间为t秒(0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S.
如图所示,已知在直角梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,1)、B(3,1).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ垂直于直线OA,垂足为Q.设P点移动的时间为t秒(0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S.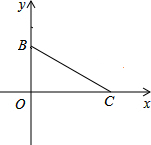 如图,B、C两点是等腰△ABC的两个顶点,在平面直角坐标系中的坐标为B(0,3),C(4,0),第三个顶点A在坐标系的x轴上,求点A的坐标.
如图,B、C两点是等腰△ABC的两个顶点,在平面直角坐标系中的坐标为B(0,3),C(4,0),第三个顶点A在坐标系的x轴上,求点A的坐标.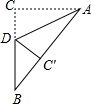 如图,在△ABC中,∠ACB=90°,AC=3,BC=4,D是BC上一点,若沿AD折叠,则点C落在AB上的点C处,求S△ABD.
如图,在△ABC中,∠ACB=90°,AC=3,BC=4,D是BC上一点,若沿AD折叠,则点C落在AB上的点C处,求S△ABD.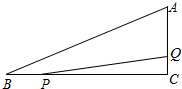 如图,在Rt△ABC中,∠C=90°,AC=5,BC=12,动点P从点B开始沿边BC向点C以每秒2个单位长度的速度运动,动点Q从点C开始沿C-A-B向点B以每秒1个单位长度的速度运动,连接PQ,点P、Q分别从点B、C同时出发,当P点到达C点时,另一点也随之停止运动,设运动时间为t秒(t≥0).
如图,在Rt△ABC中,∠C=90°,AC=5,BC=12,动点P从点B开始沿边BC向点C以每秒2个单位长度的速度运动,动点Q从点C开始沿C-A-B向点B以每秒1个单位长度的速度运动,连接PQ,点P、Q分别从点B、C同时出发,当P点到达C点时,另一点也随之停止运动,设运动时间为t秒(t≥0).