题目内容
1. 如图,PA、PB是⊙O的切线,AC是⊙O的直径,∠P=62°,则∠BOC的度数为( )
如图,PA、PB是⊙O的切线,AC是⊙O的直径,∠P=62°,则∠BOC的度数为( )| A. | 60° | B. | 62° | C. | 31° | D. | 70° |
分析 由PA、PB是⊙O的切线,根据切线的性质得到∠OAP=∠OBP=90°,再根据四边形的内角和为360°可得到∠AOB,而AC是⊙O的直径,根据互补即可得到∠BOC的度数.
解答 解:∵PA、PB是⊙O的切线,
∴∠OAP=∠OBP=90°,
而∠P=62°,
∴∠AOB=360°-90°-90°-62°=118°,
又∵AC是⊙O的直径,
∴∠BOC=180°-118°=62°.
故选B.
点评 本题考查了圆的切线的性质:圆的切线垂直于过切点的半径;也考查了四边形的内角和为360°,解题的关键是熟记切线的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.直线y=(1-2m)x+m-1,不论m取什么值,该直线必定经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
16.某公园中央地上有一个大理石球,小明想测量球的半径,于是找了两块厚20cm的砖塞在球的两侧(如图所示),他量了下两砖之间的距离刚好是80cm,聪明的你,请你算出大石头的半径是( )


| A. | 40cm | B. | 30cm | C. | 20cm | D. | 50cm |
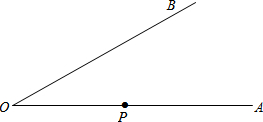 如图所示,已知∠AOB,点P在OA上.
如图所示,已知∠AOB,点P在OA上.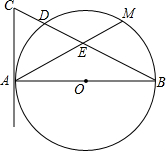 如图,AB是⊙O的直径,AC与⊙O相切于A,连接BC,BC交⊙O于点D,M是弧$\widehat{BD}$的中点,连接AM交BC于点E.
如图,AB是⊙O的直径,AC与⊙O相切于A,连接BC,BC交⊙O于点D,M是弧$\widehat{BD}$的中点,连接AM交BC于点E. 如图,两条相交线段上有9个点,一共可以组成60个不同的三角形.
如图,两条相交线段上有9个点,一共可以组成60个不同的三角形.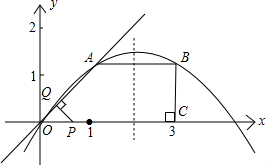 如图所示,已知在直角梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,1)、B(3,1).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ垂直于直线OA,垂足为Q.设P点移动的时间为t秒(0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S.
如图所示,已知在直角梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,1)、B(3,1).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ垂直于直线OA,垂足为Q.设P点移动的时间为t秒(0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S.