题目内容
15.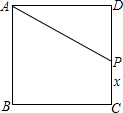 如图.正方形ABCD的边长为4cm.P为DC上的点,当点P从C向D移动时,四边形APCB的面积发生了变化.
如图.正方形ABCD的边长为4cm.P为DC上的点,当点P从C向D移动时,四边形APCB的面积发生了变化.(1)设线段CP长为x,则△APD的面积y可以表示为y=8-2x;
(2)这个变化过程中,自变量是x,因变量是y;
(3)当线段CP从1cm增加到3cm时,△APD的面积减小了多少?
分析 (1)线段CP长为x,则DP=CD-CP=4-x(cm),根据△APD的面积=$\frac{1}{2}DP•AP$,即可解答;
(2)在这个变化过程中,自变量是x,因变量是y;
(3)分别算出当CP=1cm和CP=3cm时的面积,作差即可解答.
解答 解:(1)因为线段CP长为x,则DP=CD-CP=4-x(cm),
根据△APD的面积=$\frac{1}{2}DP•AP$,
∴$y=\frac{1}{2}(4-x)×4$=8-2x.
(2)在这个变化过程中,自变量是x,因变量是y;
(3)当CP=1cm时,y=8-2×1=6(cm2),
当CP=3cm时,y=8-2×3=2(cm2),
6-2=4(cm2),
所以△APD的面积减少了4cm2.
点评 本题考查了函数关系式,解决本题的关键是由CP=x,表示出DP=4-x,根据三角形面积公式,即可解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.已知三角形的两边长分别是4和7,则这个三角形的第三条边的长可能是( )
| A. | 12 | B. | 11 | C. | 8 | D. | 3 |
 如图,两条相交线段上有9个点,一共可以组成60个不同的三角形.
如图,两条相交线段上有9个点,一共可以组成60个不同的三角形.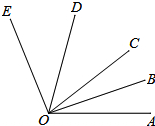 如图,∠AOE=100°,射线OD、OB是∠EOC、∠COA的角平分线.
如图,∠AOE=100°,射线OD、OB是∠EOC、∠COA的角平分线.