题目内容
 在正△ABC中,D为△ABC所在的平面内一点,当D点在平面内转动时,
在正△ABC中,D为△ABC所在的平面内一点,当D点在平面内转动时,(1)当∠BDC=60°,求∠ADB.
(2)当∠BDC=120°,求∠ADB.
考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:(1)在BD上截取DE=DC,连接CE,由∠BDC=60°,可得△EDC为正三角形,所以CE=CD,∠DCE=∠DEC=60°,然后由SAS可证△ADC≌△BEC,然后由全等三角形的对应角相等可得:∠BEC=∠ADC=120°,最后由∠BDC=60°,即可求∠ADB的度数;
(2)思路同(1),延长BD到E使DE=CD,连接CE,可得△EDC为正三角形,然后由SAS可证△ADC≌△BCE,然后由全等三角形的对应角相等可得:∠BEC=∠ADC=60°,最后由∠BDC=120°,即可求∠ADB的度数.
(2)思路同(1),延长BD到E使DE=CD,连接CE,可得△EDC为正三角形,然后由SAS可证△ADC≌△BCE,然后由全等三角形的对应角相等可得:∠BEC=∠ADC=60°,最后由∠BDC=120°,即可求∠ADB的度数.
解答:解:(1)如图1,在BD上截取DE=DC,连接CE,

∵∠BDC=60°,
∴△EDC为正三角形,
∴DC=EC,∠DCE=∠DEC=60°,
∴∠BEC=120°,
∵△ABC是正三角形,
∴AC=AB,∠ACB=60°,
∵∠BCE+∠ACE=∠ACB=60°,∠ACE+∠ACD=∠DCE=60°,
在△BCE和△ACD中,
,
∴△BCE≌△ACD(SAS),
∴∠ADC=∠BEC=120°,
∵∠BDC=60°,
∴∠ADB=∠ADC-∠BDC=120°-60°=60°;
(2)如图2,延长BD到E使DE=CD,连接CE,
∵∠BDC=120°,
∴∠CDE=60°,
∴△CDE为正三角形,
∴CD=CE,∠DCE=∠E=60°,
∵∠ACB=∠DCE=60°,
∴∠ACB+∠BCD=∠DCE+∠BCD,
即:∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴∠ADC=∠E=60°,
∵∠BDC=120°,
∴∠ADB=∠BDC-∠ADC=60°.

∵∠BDC=60°,
∴△EDC为正三角形,
∴DC=EC,∠DCE=∠DEC=60°,
∴∠BEC=120°,
∵△ABC是正三角形,
∴AC=AB,∠ACB=60°,
∵∠BCE+∠ACE=∠ACB=60°,∠ACE+∠ACD=∠DCE=60°,
在△BCE和△ACD中,
|
∴△BCE≌△ACD(SAS),
∴∠ADC=∠BEC=120°,
∵∠BDC=60°,
∴∠ADB=∠ADC-∠BDC=120°-60°=60°;
(2)如图2,延长BD到E使DE=CD,连接CE,
∵∠BDC=120°,
∴∠CDE=60°,
∴△CDE为正三角形,
∴CD=CE,∠DCE=∠E=60°,
∵∠ACB=∠DCE=60°,
∴∠ACB+∠BCD=∠DCE+∠BCD,
即:∠ACD=∠BCE,
在△ACD和△BCE中,
|
∴△ACD≌△BCE(SAS),
∴∠ADC=∠E=60°,
∵∠BDC=120°,
∴∠ADB=∠BDC-∠ADC=60°.
点评:此题考查了全等三角形的判定与性质,解题的关键是作适当辅助线,构造全等三角形.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 如图,在四边形ABED中,∠E=∠D=90°,在△ABC中,∠ACB=90°,AC=BC,其顶点C在ED上,求证:BE+AD=DE.
如图,在四边形ABED中,∠E=∠D=90°,在△ABC中,∠ACB=90°,AC=BC,其顶点C在ED上,求证:BE+AD=DE.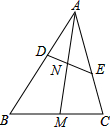 如图,在△ABC中,点D、E分别在边AB、AC上,且
如图,在△ABC中,点D、E分别在边AB、AC上,且 如图,在三角形纸片ABC中,∠C=90°,AC=6,折叠该纸片使点C落在AB边上的D点处,折痕BE与AC交于点E.若AD=BD,求折痕BE的长.
如图,在三角形纸片ABC中,∠C=90°,AC=6,折叠该纸片使点C落在AB边上的D点处,折痕BE与AC交于点E.若AD=BD,求折痕BE的长.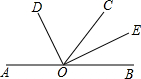 如图,O是直线AB上一点,OC为任一条射线,OD平分∠AOC,OE平分∠BOC.
如图,O是直线AB上一点,OC为任一条射线,OD平分∠AOC,OE平分∠BOC.