题目内容
12.已知点A(-1,2)和点B(3,4).试分别求出满足下列条件的点的坐标:(1)在x轴上找一点C.使得AC+BC的值最小
(2)在y轴上找一点C,使得AC+BC的值最小.
分析 (1)根据“两点之间,线段最短”可以推知,当点A、C、B三点共线时,AC+BC的值最小.所以作B关于x轴的对称点B′,连结AB′交x轴于点C.点C即为所求;
(2)根据“两点之间,线段最短”可以推知,当点A、C、B三点共线时,AC+BC的值最小.由于连接AB交y轴于C,即可得到结果.
解答  解:(1)C点如图1所示(或作B关于x轴的对称点B′,连结AB′交x轴于点C).
解:(1)C点如图1所示(或作B关于x轴的对称点B′,连结AB′交x轴于点C).
设直线AB′的解析式为y=kx+b(k≠0).
∵B(3,4),
∴B′(3,-4).
又∵A(-1,2),
∴$\left\{\begin{array}{l}{-4=3k+b}\\{2=-k+b}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{k=-\frac{3}{2}}\\{b=\frac{1}{2}}\end{array}\right.$,
∴AB′直线解析式:y=-$\frac{3}{2}$x+$\frac{1}{2}$,
∴点C的坐标为($\frac{1}{3}$,0);
(2)C点如图2所示,连接AB交y轴于C,
则点C即为所求.
点评 本题考查了轴对称-最短距离问题,坐标与图形的性质,正确的作出图形是解题的关键.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
2.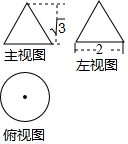 已知一个圆锥的三视图如图所示,请利用图中所给出数据,求出这个圆锥的侧面积为( )
已知一个圆锥的三视图如图所示,请利用图中所给出数据,求出这个圆锥的侧面积为( )
 已知一个圆锥的三视图如图所示,请利用图中所给出数据,求出这个圆锥的侧面积为( )
已知一个圆锥的三视图如图所示,请利用图中所给出数据,求出这个圆锥的侧面积为( )| A. | 2π | B. | 4π | C. | $\sqrt{3}$π | D. | 2$\sqrt{3}$π |
3. 如图,将△ABC绕点C(0,1)旋转180°得到△DEC.若点A的坐标为(3,-1),则点D的坐标为( )
如图,将△ABC绕点C(0,1)旋转180°得到△DEC.若点A的坐标为(3,-1),则点D的坐标为( )
 如图,将△ABC绕点C(0,1)旋转180°得到△DEC.若点A的坐标为(3,-1),则点D的坐标为( )
如图,将△ABC绕点C(0,1)旋转180°得到△DEC.若点A的坐标为(3,-1),则点D的坐标为( )| A. | (-3,1) | B. | (-2,2) | C. | (-3,3) | D. | (-3,2) |
4.下列计算中,正确的是( )
| A. | x4•x2=x8 | B. | x4÷x2=x6 | C. | (x4)2=x8 | D. | (3x)2=3x2 |
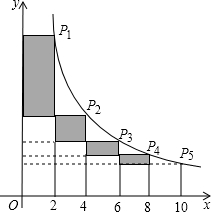 如图,在反比例函数y=$\frac{5}{x}$(x>0)的图象上有点P1、P2、P3、P4,P5,它们的横坐标依次为2,4,6,8,10,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,S4,则S1+S2+S3+S4的值为( )
如图,在反比例函数y=$\frac{5}{x}$(x>0)的图象上有点P1、P2、P3、P4,P5,它们的横坐标依次为2,4,6,8,10,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,S4,则S1+S2+S3+S4的值为( )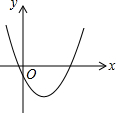 如图的抛物线是把抛物线y=$\frac{1}{2}$x2平移后经过(0,-1)和(4,-1)两点得到的.
如图的抛物线是把抛物线y=$\frac{1}{2}$x2平移后经过(0,-1)和(4,-1)两点得到的.