题目内容
2.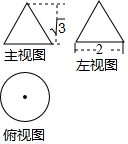 已知一个圆锥的三视图如图所示,请利用图中所给出数据,求出这个圆锥的侧面积为( )
已知一个圆锥的三视图如图所示,请利用图中所给出数据,求出这个圆锥的侧面积为( )| A. | 2π | B. | 4π | C. | $\sqrt{3}$π | D. | 2$\sqrt{3}$π |
分析 先利用三视图得到底面圆的半径为1,圆锥的高为$\sqrt{3}$,再根据勾股定理计算出母线长为2,然后根据锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式计算.
解答 解:根据三视图得到圆锥的底面圆的直径为2,即底面圆的半径为1,圆锥的高为$\sqrt{3}$,
所以圆锥的母线长=$\sqrt{(\sqrt{3})^{2}+{1}^{2}}$=2,
所以这个圆锥的侧面积=$\frac{1}{2}$•2π•1•2=2π.
故选A.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.也考查了三视图.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
14.下列说法正确的是( )
| A. | 抛掷一个正方体骰子,点数为奇数的概率是$\frac{1}{3}$ | |
| B. | 买一张福利彩票一定中奖,是不可能事件 | |
| C. | 在地球上,上抛的篮球一定会下落,是必然事件 | |
| D. | 从一个装有5个黑球和1个红球的口袋中,摸出一个球是黑球是必然事件 |
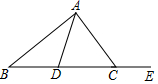 已知:如图,AD是△ABC的中线,∠ACE是△ABC的外角.
已知:如图,AD是△ABC的中线,∠ACE是△ABC的外角. 水果市场的甲、乙两家商店中都有批发某种水果,批发该种水果x千克时,在甲、乙两家商店所花的钱分别为y1元和y2元,已知y1、y2关于x的函数图象分别为如图所示的折线OAB和射线OC.
水果市场的甲、乙两家商店中都有批发某种水果,批发该种水果x千克时,在甲、乙两家商店所花的钱分别为y1元和y2元,已知y1、y2关于x的函数图象分别为如图所示的折线OAB和射线OC.