题目内容
11.计算:|$\sqrt{3}$-2|=2-$\sqrt{3}$(结果保留根号);若|a|=$\sqrt{2}$,则a=$±\sqrt{2}$,化简$\sqrt{(-4)^{2}}$=4.分析 根据差的绝对值是大数减小数,可得答案;
根据互为相反数的绝对值相等,可得答案;
根据二次根式的性质,可得答案.
解答 解:|$\sqrt{3}$-2|═2-$\sqrt{3}$,;若|a|=$\sqrt{2}$,则a=$±\sqrt{2}$;$\sqrt{(-4)^{2}}$=$\sqrt{{4}^{2}}$=4,
故答案为:2-$\sqrt{3}$,$±\sqrt{2}$,4.
点评 本题考查了实数的性质,差的绝对值是大数减小数,注意互为相反数的绝对值相等.

练习册系列答案
相关题目
1.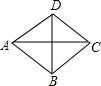 如图,菱形ABCD中,AC=8,BD=6,则菱形的面积为( )
如图,菱形ABCD中,AC=8,BD=6,则菱形的面积为( )
 如图,菱形ABCD中,AC=8,BD=6,则菱形的面积为( )
如图,菱形ABCD中,AC=8,BD=6,则菱形的面积为( )| A. | 10 | B. | 20 | C. | 48 | D. | 24 |
6.已知a为任何实数,那么下列各式一定有意义的是( )
| A. | $\sqrt{{a}^{2}-1}$ | B. | $\sqrt{{a}^{2}+1}$ | C. | $\sqrt{\frac{1}{(a-1)^{2}}}$ | D. | $\sqrt{\frac{1}{(a+1)^{2}}}$ |
16.如果代数式y2-2y+3的值为2,那么代数式2y2-4y+1的值为( )
| A. | -4 | B. | -1 | C. | 0 | D. | 4 |
3.某人沿着坡度i=1:$\sqrt{3}$的山坡走了50米,则他离地面的高度( )
| A. | 50m | B. | 50$\sqrt{3}$m | C. | 25m | D. | 25$\sqrt{3}$m |
 (1)(-$\frac{1}{2}$)-2+|$\sqrt{3}$-3|-$\root{3}{27}$+tan60°
(1)(-$\frac{1}{2}$)-2+|$\sqrt{3}$-3|-$\root{3}{27}$+tan60°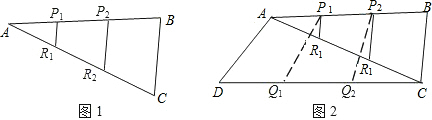
 某住宅小区为缓解停车难问题,新建了地下停车场,建筑设计师提供了地下停车场的设计示意图.按规定,停车场坡道口要张贴限高标志,以便告知车辆能否安全驶入.请根据如图,求出汽车通过坡道口的限高CF的长($\sqrt{3}$≈1.73,结果精确到0.1m).
某住宅小区为缓解停车难问题,新建了地下停车场,建筑设计师提供了地下停车场的设计示意图.按规定,停车场坡道口要张贴限高标志,以便告知车辆能否安全驶入.请根据如图,求出汽车通过坡道口的限高CF的长($\sqrt{3}$≈1.73,结果精确到0.1m).