题目内容
20.某课题研究小组就图形面积问题进行专题研究,他们发现如下结论:(1)有一条边对应相等的两个三角形的面积之比等于这条边上的对应高之比;
(2)有一个角对应相等的两个三角形的面积之比等于夹这个角的两边乘积之比;…
现请你继续下面问题的探究,探究过程可直接应用上述结论.(S表示面积)
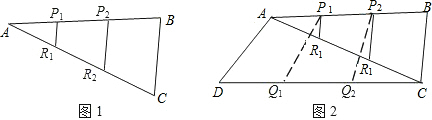
问题1:如图1,现有一块三角形纸板ABC,P1,P2三等分边AB,R1,R2三等分边AC.经探究知
S${\;}_{四边形P{{\;}_{1}R}_{1}R{{\;}_{2}P}_{2}}$=$\frac{1}{3}$S△ABC,请证明.
问题2:若有另一块三角形纸板,可将其与问题1中的△ABC拼合成四边形ABCD,如图2,Q1,Q2三等分边DC.试探究S${\;}_{四边形{P}_{1}{Q}_{1}{Q}_{2}{P}_{2}}$与S四边形ABCD之间的数量关系.
分析 问题1,图1中,连接P1R2,R2B,由三角形中线的性质得S△AP1R1=S△P1R1R2,S△P1R2P2=S△P2R2B,再由R1,R2为AC的三等分点,得S△BCR2=$\frac{1}{2}$S△ABR2,根据图形的面积关系,得S△ABC与S四边形P1R1R2P2的数量关系,证明结论;
问题2,图2中,连接AQ1,Q1P2,P2C,由三角形的中线性质,得S△AQ1P1=S△P1Q1P2,S△P2Q1Q2=S△P2Q2C,由Q1,P2为CD,AB的三等分点可知:S△ADQ1=$\frac{1}{2}$S△AQ1C,S△BCP2=$\frac{1}{2}$S△AP2C,得出S△ADQ1+S△BCP2与S四边形AQ1CP2的关系,再根据图形的面积关系,得S四边形ABCD与S四边形P1Q1Q2P2的等量关系.
解答 证明:问题1, 如图1,连接P1R2,R2B,在△AP1R2中,
如图1,连接P1R2,R2B,在△AP1R2中,
∵P1R1为中线,
∴S△AP1R1=S△P1R1R2,
同理S△P1R2P2=S△P2R2B,
∴S△P1R1R2+S△P1R2P2=$\frac{1}{2}$S△ABR2=S四边形P1P2R2R1,
由R1,R2为AC的三等分点可知,
S△BCR2=$\frac{1}{2}$S△ABR2,
∴S△ABC=S△BCR2+S△ABR2=S四边形P1P2R2R1+2S四边形P1P2R2R1=3S四边形P1P2R2R1,
∴S四边形P1R1R2P2=$\frac{1}{3}$S△ABC;
解:问题2,S四边形ABCD=3S四边形P1Q1Q2P2.
理由:如图2,连接AQ1,Q1P2,P2C,在△AQ1P2中,
∵Q1P1为中线,
∴S△AQ1P1=S△P1Q1P2,
同理S△P2Q1Q2=S△P2Q2C,
∴S△P1Q1P2+S△P2Q1Q2=$\frac{1}{2}$S四边形AQ1CP2=S四边形P1Q1Q2P2,
由Q1,P2为CD,AB的三等分点可知,
S△ADQ1=$\frac{1}{2}$S△AQ1C,S△BCP2=$\frac{1}{2}$S△AP2C,
∴S△ADQ1+S△BCP2=$\frac{1}{2}$(S△AQ1C+S△AP2C)=$\frac{1}{2}$S四边形AQ1CP2,
∴S四边形ABCD=S△ADC+S△ABC=S四边形AQ1CP2+S△ADQ1+S△BCP2=3S四边形P1Q1Q2P2,
即S四边形ABCD=3S四边形P1Q1Q2P2.
点评 本题考查了面积与等积变换问题,关键是利用三角形的中线把三角形分为面积相等的两个三角形的性质进行推理.

| A. | 357×104 | B. | 3.57×107 | C. | 35.7×105 | D. | 3.57×106 |