��Ŀ����
19��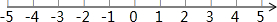 ��1����-$\frac{1}{2}$��-2+|$\sqrt{3}$-3|-$\root{3}{27}$+tan60��
��1����-$\frac{1}{2}$��-2+|$\sqrt{3}$-3|-$\root{3}{27}$+tan60����2���ⲻ��ʽ�飬�������Ľ⼯�������ϱ�ʾ������
$\left\{\begin{array}{l}{5x-1��3��x+1��}\\{\frac{2x-1}{3}-\frac{5x+1}{2}��1}\end{array}\right.$
��3���Ȼ�������ֵ��$\frac{{x}^{2}-1}{x+2}$�£�1-$\frac{1}{x+2}$��������x��ֵ���㣺x2=4��
���� ��1���ֱ���ݸ�����ָ���ݵļ��㷨�����Ŀ�����������ǵ����Ǻ���ֵ������������ٸ���ʵ���������ķ�����м��㼴�ɣ�
��2���ֱ����������ʽ�Ľ⼯��������乫���⼯�����������ϱ�ʾ�������ɣ�
��3���ȸ��ݷ�ʽ�������ķ����ԭʽ���л��������x��ֵ������м��㼴�ɣ�
��� �⣺��1��ԭʽ=4+3-$\sqrt{3}$-3+$\sqrt{3}$
=4��
��2��$\left\{\begin{array}{l}5x-1��3��x+1����\\ \frac{2x-1}{3}-\frac{5x+1}{2}��1��\end{array}\right.$���ɢٵã�x��2���ɢڵã�x��-1��
�ʲ���ʽ��Ľ⼯Ϊ��-1��x��2��
�������ϱ�ʾΪ�� ��
��
��3��ԭʽ=$\frac{{x}^{2}-1}{x+2}$��$\frac{x+1}{x+2}$
=$\frac{��x+1����x-1��}{x+2}$•$\frac{x+2}{x+1}$
=x-1��
��x2=4�ã�x=��2��
��x+2��0��
��x��-2��
�൱x=2ʱ��ԭʽ=1��
���� ���⿼����Ƿ�ʽ�Ļ�����ֵ����֪��ʽ�������ķ����ǽ�����Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
9��Ҫʹ��ʽ$\frac{x+2}{x-1}$�����壬��x��ȡֵӦ���㣨������
| A�� | x��-2 | B�� | x��1 | C�� | x=-2 | D�� | x=1 |
7���������㣺��1��2x3-x2=x����2��x3•��x5��2=x13����3����-x��6�£�-x��3=x3����4����-2x3y��2=4x6y2��������ȷ���ǣ�������
| A�� | ��1����2�� | B�� | ��2����4�� | C�� | ��2����3�� | D�� | ��3����4�� |
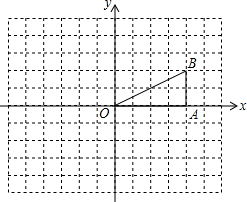 ��ͼ���ڡ�OAB�У���OAB=90�㣬�ҵ�B������Ϊ��4��2����
��ͼ���ڡ�OAB�У���OAB=90�㣬�ҵ�B������Ϊ��4��2����