题目内容
如图，⊙O的直径为4，弦AB垂直平分半径OC，则四边形OACB的周长为（ ）| A、8 | B、12 | C、16 | D、20 |
考点：垂径定理,勾股定理
专题：
分析：由AB垂直平分OC可知，OA=AC，而半径OA=OC，可证△OAC为等边三角形，四边形OACB为菱形，由此可得出结论．
解答：解：∵⊙O的直径为4，
∴OA=OB=OC=2．
∵AB垂直平分OC，
∴OA=AC，
又∵半径OA=OC=2，
∴△OAC为等边三角形，四边形OACB为菱形，
∴四边形OACB的周长=8．
故选A．
∴OA=OB=OC=2．
∵AB垂直平分OC，
∴OA=AC，
又∵半径OA=OC=2，
∴△OAC为等边三角形，四边形OACB为菱形，
∴四边形OACB的周长=8．
故选A．
点评：本题考查的是垂径定理，熟知平分弦的直径平分这条弦，并且平分弦所对的两条弧是解答此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
如图：AB⊥CD，CD为⊙O直径，且AB=20，CE=4，那么⊙O的半径是（ ）A、
| ||
| B、14 | ||
C、
| ||
| D、15 |
掷一次骰子（毎面分别刻有1-6点），向上一面的点数是奇数的概率等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，AB是⊙O的直径，C、D是⊙O上两点，CD⊥AB，若∠DAB=65°，则∠AOC等于（ ）| A、25° | B、30° |
| C、50° | D、65° |
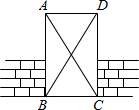如图所示，工人师傅将门砌到一定高度时，质检员要测一下门的四个角是否都为直角，请你帮质检员想一个检测的办法，并说明理由．
如图，在平行四边形ABCD中，∠BDA=90°，AC=10，BD=6，则AD=（ ）| A、4 | B、5 | C、6 | D、8 |
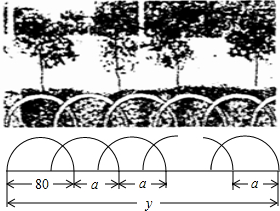如图，某花园护栏是用直径为80厘米的半圆形条钢组制而成，且每增加一个半圆形条钢，护栏长度就增加a厘米（a＞0）．设半圆形条钢的总个数为x（x为正整数），护栏总长度为y厘米．
如图，直线l1：y=ax，l2：y=kx+b相交于点A，则关于x，y的二元一次方程组