题目内容
两个水平相当的选手在决赛中相遇,决赛采用五局三胜制,胜者获得全部奖金,前三局打成2:1时比赛因故终止.有人提出按2:1分配奖金,你认为这样合理吗?
考点:概率的意义
专题:
分析:根据后两局获胜的概率,可得答案.
解答:解:奖金应按2:1分配不合理,
设甲乙两队前三局是2:1,
最后2局出现的可能情况为:
甲胜、甲胜;
甲胜、乙胜;
乙胜、甲胜;
乙胜、乙胜.
其中乙必须获胜二局才行,故乙获胜的概率是
,
甲获胜的概率是
,
奖金应按3:1分配合理.
设甲乙两队前三局是2:1,
最后2局出现的可能情况为:
甲胜、甲胜;
甲胜、乙胜;
乙胜、甲胜;
乙胜、乙胜.
其中乙必须获胜二局才行,故乙获胜的概率是
| 1 |
| 4 |
甲获胜的概率是
| 3 |
| 4 |
奖金应按3:1分配合理.
点评:本题考查了概率的意义,列出后两局可能出现的结果,再得出甲获胜的概率.

练习册系列答案
相关题目
若在同一个坐标系中作出下列直线:①y=-
x-1;②y=2x-1;③y=-
x+1;④y=x-1,那么相互平行直线是( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、①③ | B、②④ | C、①② | D、①④ |
 如图,△ABC绕点A顺时针旋转60°得到△AEF,若∠B=100°,∠F=50°,则∠CAE的度数为
如图,△ABC绕点A顺时针旋转60°得到△AEF,若∠B=100°,∠F=50°,则∠CAE的度数为 已知,如图,AB为⊙O的直径,E为⊙O外一点,EB,EC分别切⊙O于点B,C,求证:AC∥OE.
已知,如图,AB为⊙O的直径,E为⊙O外一点,EB,EC分别切⊙O于点B,C,求证:AC∥OE.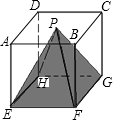 一个边长为5厘米的正方体,它是由125个边长为1厘米的小正方体组成的,P为上底面ABCD的中心,如果挖去的阴影部分为四棱锥,剩下的部分还包括多少个完整的棱长是1厘米的小正方体?
一个边长为5厘米的正方体,它是由125个边长为1厘米的小正方体组成的,P为上底面ABCD的中心,如果挖去的阴影部分为四棱锥,剩下的部分还包括多少个完整的棱长是1厘米的小正方体?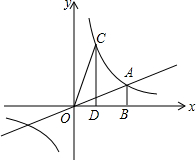 如图,直线y=
如图,直线y=