题目内容
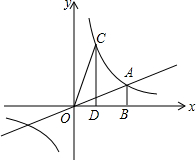 如图,直线y=
如图,直线y=| 1 |
| 2 |
| k |
| x |
| k |
| x |
(1)求k的值.
(2)设△COD与△AOB的重合部分的面积为S,求S关于m的函数解析式.
(3)连接AC,当第(2)问中S的值为1时,求△OAC的面积.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)由题意列出关于k的方程,求出k的值,即可解决问题.
(2)借助函数解析式,运用字母m表示DE、OD的长度,即可解决问题.
(3)首先求出m的值,求出△COD,△AOB的面积;求出梯形ABDC的面积,即可解决问题.
(2)借助函数解析式,运用字母m表示DE、OD的长度,即可解决问题.
(3)首先求出m的值,求出△COD,△AOB的面积;求出梯形ABDC的面积,即可解决问题.
解答: 解:(1)设A点的坐标为(4,λ);
解:(1)设A点的坐标为(4,λ);
由题意得:
,解得:k=8,
即k的值=8.
(2)如图,设E点的坐标为E(m,n).
则n=
m,即DE=
m;而OD=m,
∴S=
OD•DE=
m×
m=
m2,
即S关于m的函数解析式是S=
m2.
(3)当S=1时,
m2=1,解得m=2或-2(舍去),
∵点C在函数y=
的图象上,
∴CD=
=4;由(1)知:
OB=4,AB=2;BD=4-2=2;
∴S梯形ABDC=
(4+2)×2=6,
S△AOB=
×4×2=4,
S△COD=
×2×4=4;
∴S△AOC=S梯形ABDC+S△COD-S△AOB
=6+4-4=6.
 解:(1)设A点的坐标为(4,λ);
解:(1)设A点的坐标为(4,λ);由题意得:
|
即k的值=8.
(2)如图,设E点的坐标为E(m,n).
则n=
| 1 |
| 2 |
| 1 |
| 2 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
即S关于m的函数解析式是S=
| 1 |
| 4 |
(3)当S=1时,
| 1 |
| 4 |
∵点C在函数y=
| 8 |
| x |
∴CD=
| 8 |
| 2 |
OB=4,AB=2;BD=4-2=2;
∴S梯形ABDC=
| 1 |
| 2 |
S△AOB=
| 1 |
| 2 |
S△COD=
| 1 |
| 2 |
∴S△AOC=S梯形ABDC+S△COD-S△AOB
=6+4-4=6.
点评:该题主要考查了一次函数与反比例函数图象的交点问题;解题的关键是数形结合,灵活运用方程、函数等知识来分析、判断、求解或证明.

练习册系列答案
相关题目
方程组
(a为常数)的解满足方程x-y=3,则原方程组的解是( )
|
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
直线y=3x与x轴正半轴的夹角的锐角为α,那么下列结论正确的是( )
| A、tanα=3 | ||
B、tanα=
| ||
| C、sinα=3 | ||
| D、cosα=3 |
若线段的长x是3和6的比例中项,则x的值为( )
A、3
| ||
B、-3
| ||
C、±3
| ||
D、±2
|