题目内容
8.计算:$\sqrt{48}$+3$\sqrt{\frac{1}{3}}$-2$\sqrt{27}$=-$\sqrt{3}$.分析 利用二次根式的性质化简进而合并求出即可.
解答 解:$\sqrt{48}$+3$\sqrt{\frac{1}{3}}$-2$\sqrt{27}$=4$\sqrt{3}$+3×$\frac{\sqrt{3}}{3}$-6$\sqrt{3}$=-$\sqrt{3}$.
故答案为:-$\sqrt{3}$.
点评 此题主要考查了二次根式的加减运算,正确化简二次根式是解题关键.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
16.一个直角三角形的两直角边长分别为3,4,则第三边长是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 5或$\sqrt{7}$ |
3.已知:点P的坐标为(-2,1),则点P所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
20.下列说法中,错误的是( )
| A. | 不等式x<2的正整数解有一个 | B. | -2是不等式2x-1<0的一个解 | ||
| C. | 不等式x<10的整数解有无数个 | D. | 不等式2x>-6的解集是x<-3 |
17.下列语句中,假命题是( )
| A. | 如果直线a,b,c满足a∥b,b∥c,那么a∥c | |
| B. | 三角形的内角和为180° | |
| C. | 内错角相等 | |
| D. | 对顶角相等 |
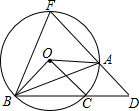 如图,已知△ABC内接于⊙O,∠BOC=2∠AOC,过点A作直线DF∥OC,交BC的延长线于点D,交⊙O于点F,连接BF.
如图,已知△ABC内接于⊙O,∠BOC=2∠AOC,过点A作直线DF∥OC,交BC的延长线于点D,交⊙O于点F,连接BF.