题目内容
13.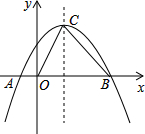 如图,二次函数y=ax2+bx+c图象的顶点坐标为(2,3),与x轴交于点A(-1,0).
如图,二次函数y=ax2+bx+c图象的顶点坐标为(2,3),与x轴交于点A(-1,0).(1)求二次函数的解析式;
(2)连结BC、OC,在抛物线的对称轴上是否存在点P,使得以P、B、C为顶点的三角形与△OBC相似?若存在点P,求出点P的坐标;若不存在,请说明理由.
分析 (1)利用待定系数法即可求得二次函数的解析式;
(2)求得B(5,0),如图,设对称轴与x轴交点为D,则CD=BD=3,得到∠DCB=∠DBC=45°求得BC=3$\sqrt{2}$设P(2,t),①当△PCB∽△OBC时,则$\frac{PC}{OB}=\frac{CB}{BC}$=1,求得t=-2得到P(2,-2);②当△BCP∽△OBC时,列比例式求得t=-$\frac{3}{5}$,即可得到P(2,-$\frac{3}{5}$).
解答 解:(1)∵二次函数y=ax2+bx+c图象的顶点坐标为(2,3),
∴设二次函数的解析式为:y=a(x-2)2+3,将(-1,0)点代入得:a=-$\frac{1}{3}$,
故二次函数的解析式为:y=-$\frac{1}{3}$(x-2)2+3
∴y=-$\frac{1}{3}$x2+$\frac{4}{3}$x$+\frac{5}{3}$;
(2)存在,
在y=-$\frac{1}{3}$x2+$\frac{4}{3}$x$+\frac{5}{3}$中,令y=0,则-$\frac{1}{3}$x2+$\frac{4}{3}$x$+\frac{5}{3}$=0,解得:x1=-1,x2=5,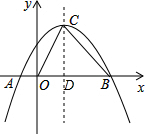
∴B(5,0),
∵抛物线的对称轴方程为:x=2,
如图,设对称轴与x轴交点为D,则CD=BD=3,
∴∠DCB=∠DBC=45°
∴BC=3$\sqrt{2}$
设P(2,t),
①当△PCB∽△OBC时,则$\frac{PC}{OB}=\frac{CB}{BC}$=1,
∴PC=OB,即3-t=5,
∴t=-2,∴P(2,-2);
②当△BCP∽△OBC时,则$\frac{BC}{OB}=\frac{CP}{BC}$,即$\frac{3\sqrt{2}}{5}=\frac{3-t}{3\sqrt{2}}$,
∴t=-$\frac{3}{5}$,
∴P(2,-$\frac{3}{5}$),
综上所述:存在点P,使得以P、B、C为顶点的三角形与△OBC相似,点P的坐标为(2,-2),(2,-$\frac{3}{5}$).
点评 本题考查了待定系数法求二次函数的解析式,相似三角形的性质,等腰直角三角形的性质,勾股定理,找准三角形相似是解题的关键.

 阅读快车系列答案
阅读快车系列答案
| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
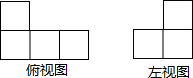 如图,这是由若干个相同的小立方体搭成的几何体俯视图和左视图,则小立方体的个数可能是5个或6个或7个.
如图,这是由若干个相同的小立方体搭成的几何体俯视图和左视图,则小立方体的个数可能是5个或6个或7个.
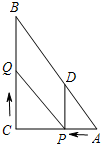 如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,动点P从点A开始,沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始,沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连结PQ.点P,Q分别从点A,C同时出发,当其中一点到达端点时,另两个点也随之停止运动,设运动时间为t秒(t≥0).
如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,动点P从点A开始,沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始,沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连结PQ.点P,Q分别从点A,C同时出发,当其中一点到达端点时,另两个点也随之停止运动,设运动时间为t秒(t≥0).