题目内容
16.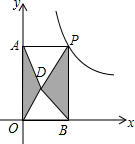 如图,点P是反比例函数y=$\frac{6}{x}$(x>0)的图象上的任意一点,过点P分别作两坐标轴的垂线,与坐标轴构成矩形OAPB,点D是矩形OAPB内任意一点,连接DA、DB、DP、DO,则图中阴影部分的面积是( )
如图,点P是反比例函数y=$\frac{6}{x}$(x>0)的图象上的任意一点,过点P分别作两坐标轴的垂线,与坐标轴构成矩形OAPB,点D是矩形OAPB内任意一点,连接DA、DB、DP、DO,则图中阴影部分的面积是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4. |
分析 首先根据反比例系数k的几何意义,可知矩形OAPB的面积=6,然后根据题意,得出图中阴影部分的面积是矩形OAPB的面积的一半,从而求出结果.
解答 解:∵P是反比例函数$\frac{6}{x}$的图象的任意点,过点P分别做两坐标轴的垂线,
∴与坐标轴构成矩形OAPB的面积=6.
∴阴影部分的面积=$\frac{1}{2}$×矩形OAPB的面积=3.
故选C.
点评 本题考查了反比例函数比例系数k的几何意义和矩形的性质,在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|是解答此题的关键.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
7.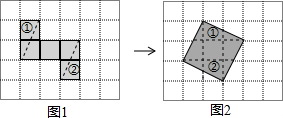 如图1,每个小正方形的边长均为1,按虚线把阴影部分剪下来,用剪下来的阴影部分重新拼成如图2所示的正方形,那么所拼成的正方形的边长为( )
如图1,每个小正方形的边长均为1,按虚线把阴影部分剪下来,用剪下来的阴影部分重新拼成如图2所示的正方形,那么所拼成的正方形的边长为( )
 如图1,每个小正方形的边长均为1,按虚线把阴影部分剪下来,用剪下来的阴影部分重新拼成如图2所示的正方形,那么所拼成的正方形的边长为( )
如图1,每个小正方形的边长均为1,按虚线把阴影部分剪下来,用剪下来的阴影部分重新拼成如图2所示的正方形,那么所拼成的正方形的边长为( )| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{6}$ |
8.下列根式中,与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{8}$ | C. | $\sqrt{6}$ | D. | $\sqrt{5}$ |
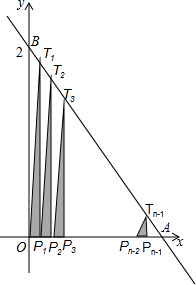 如图,直线y=-2x+2与两坐标轴分别交于A、B两点,将线段OA分成n等份,分点分别为P1,P2,P3,…,Pn-1,过每个分点作x轴的垂线分别交直线AB于点T1,T2,T3,…,Tn-1,用S1,S2,S3,…,Sn-1分别表示Rt△T1OP1,Rt△T2P1P2,…,Rt△Tn-1Pn-2Pn-1的面积,则当n=2015时,S1+S2+S3+…+Sn-1=$\frac{1007}{2015}$.
如图,直线y=-2x+2与两坐标轴分别交于A、B两点,将线段OA分成n等份,分点分别为P1,P2,P3,…,Pn-1,过每个分点作x轴的垂线分别交直线AB于点T1,T2,T3,…,Tn-1,用S1,S2,S3,…,Sn-1分别表示Rt△T1OP1,Rt△T2P1P2,…,Rt△Tn-1Pn-2Pn-1的面积,则当n=2015时,S1+S2+S3+…+Sn-1=$\frac{1007}{2015}$. 如图,直线AB,CD相交于点O,OA平分∠EOC,若∠EOC:∠EOD=2:3,∠BOD=36度.
如图,直线AB,CD相交于点O,OA平分∠EOC,若∠EOC:∠EOD=2:3,∠BOD=36度.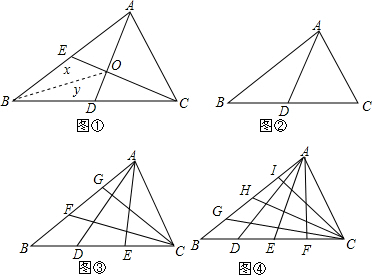
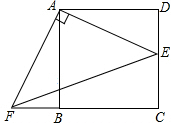 如图,已知点E是正方形ABCD边CD上的一点,点F在CB的延长线上,且DE=BF.求证:△AFE是等腰直角三角形.
如图,已知点E是正方形ABCD边CD上的一点,点F在CB的延长线上,且DE=BF.求证:△AFE是等腰直角三角形. 如图,矩形ABCD中,AB=4,BC=6,P是CD边上的中点,E是BC边上的一动点,M,N分别是AE、PE的中点,则随着点E的运动,线段MN长的取值或取值范围为$\sqrt{10}$.
如图,矩形ABCD中,AB=4,BC=6,P是CD边上的中点,E是BC边上的一动点,M,N分别是AE、PE的中点,则随着点E的运动,线段MN长的取值或取值范围为$\sqrt{10}$.