题目内容
5．已知a=$\sqrt{3}$-1，b=$\sqrt{3}$+1，计算式子a2+b2的值为8．分析 首先求得a+b与ab的数值，再根据完全平方公式变形：a2+b2=（a+b）2-2ab，最后整体代入求出即可．
解答 解：∵a=$\sqrt{3}$-1，b=$\sqrt{3}$+1，
∴a+b=2$\sqrt{3}$，ab=2，
∴a2+b2=（a+b）2-2ab=（2$\sqrt{3}$）2-2×2=8．
故答案为：8．
点评 本题考查了二次根式的化简求值，完全平方公式的应用，注意：完全平方公式是：（a+b）+2=a2+2ab+b2，（a-b）2=a2-2ab+b2．
练习册系列答案
阅读快车系列答案
相关题目
15．函数$\frac{1}{2}$≤x≤2时，$\frac{1}{4}$≤y≤1，则这个函数可以是（ ）
| A． | y=$\frac{1}{2x}$ | B． | y=$\frac{2}{x}$ | C． | y=$\frac{1}{8x}$ | D． | y=$\frac{8}{x}$ |
16．
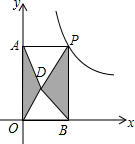如图，点P是反比例函数y=$\frac{6}{x}$（x＞0）的图象上的任意一点，过点P分别作两坐标轴的垂线，与坐标轴构成矩形OAPB，点D是矩形OAPB内任意一点，连接DA、DB、DP、DO，则图中阴影部分的面积是（ ）
如图，点P是反比例函数y=$\frac{6}{x}$（x＞0）的图象上的任意一点，过点P分别作两坐标轴的垂线，与坐标轴构成矩形OAPB，点D是矩形OAPB内任意一点，连接DA、DB、DP、DO，则图中阴影部分的面积是（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4． |
如图，AB∥CD，E、F分别在AB、CD上，若∠1+∠D=180°，那么EF与BD平行吗？为什么？
20．在平面直角坐标系中，如果点P（a，2）在第二象限，那么点Q（-3，a）在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
如图，在矩形ABCD中，对角线AC与BD相交于点O，AE垂直且平分线段BO，垂足为点E，BD=15cm，求AC、AB的长．