题目内容
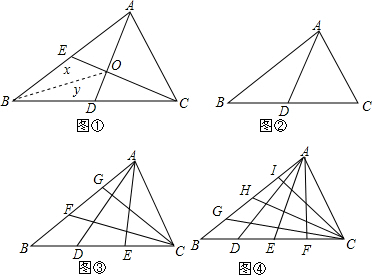
11.(1)如图①,AD是△ABC的中线,△ABD与△ACD的面积有怎样的数量关系?为什么?(2)若三角形的面积记为S,例如:△ABC的面积记为S△ABC,如图②,已知S△ABC=1,△ABC的中线AD、CE相交于点O,求四边形BDOE的面积.
小华利用(1)的结论,解决了上述问题,解法如下:
连接BO,设S△BEO=x,S△BDO=y,
由(1)结论可得:S${\;}_{△BCE}={S}_{ABD}=\frac{1}{2}{S}_{△ABC}=\frac{1}{2}$,
S△BCO=2S△BDO=2y,
S△BAO=2S△BEO=2x.
则有$\left\{\begin{array}{l}{{S}_{△BEO}+{S}_{△BCO}={S}_{△BCE}}\\{{S}_{△BAO}+{S}_{△BDO}={S}_{△BAD}}\end{array}\right.$,即$\left\{\begin{array}{l}{x+2y=\frac{1}{2}}\\{2x+y=\frac{1}{2}}\end{array}\right.$.
所以$x+y=\frac{1}{3}.即四边形BDOE面积为\frac{1}{3}$.
请仿照上面的方法,解决下列问题:
①如图③,已知S△ABC=1,D、E是BC边上的三等分点,F、G是AB边上的三等分点,AD、CF交于点O,求四边形BDOF的面积.
②如图④,已知S△ABC=1,D、E、F是BC边上的四等分点,G、H、I是AB边上的四等分点,AD、CG交于点O,则四边形BDOG的面积为$\frac{1}{10}$.
分析 (1)利用等底等高的三角形面积相等求解即可;
(2)①连接BO,设S△BDO=x,S△BGO=y,根据三角形间的面积关系列出方程组求解即可;
②连接BO,设S△BDO=x,S△BGO=y,根据三角形间的面积关系列出方程组求解即可.
解答 解:(1)S△ABD=S△ACD.
∵AD是△ABC的中线,
∴BD=CD,
又∵△ABD与△ACD高相等,
∴S△ABD=S△ACD.
(2)①如图3,连接BO,设S△BFO=x,S△BDO=y,
S△BCF=S△ABD=$\frac{1}{3}$S△ABC=$\frac{1}{3}$
S△BCO=3S△BDO=3y,
S△BAO=3S△BFO=3x.
则有$\left\{\begin{array}{l}{{S}_{△BFO}+{S}_{△BCO}={S}_{△BCF}}\\{{S}_{△BDO}+{S}_{△BAO}={S}_{△ABD}}\end{array}\right.$,即$\left\{\begin{array}{l}{x+3y=\frac{1}{3}}\\{y+3x=\frac{1}{3}}\end{array}\right.$,
所以x+y=$\frac{1}{6}$,即四边形BDOF的面积为$\frac{1}{6}$;
②如图,连接BO,设S△BDO=x,S△BGO=y,
S△BCG=S△ABD=$\frac{1}{4}$S△ABC=$\frac{1}{4}$,
S△BCO=4S△BDO=4x,
S△BAO=4S△BGO=4y.
则有$\left\{\begin{array}{l}{{S}_{△BDO}+{S}_{△AOB}={S}_{△ABD}}\\{{S}_{△BGO}+{S}_{△BCO}={S}_{△BCG}}\end{array}\right.$,即$\left\{\begin{array}{l}{x+4y=\frac{1}{4}}\\{y+4x=\frac{1}{4}}\end{array}\right.$,
所以x+y=$\frac{1}{10}$,即四边形BDOG的面积为$\frac{1}{10}$,
故答案为:$\frac{1}{10}$.
点评 本题主要考查了面积与等积变换,等底等高的三角形的面积相等等知识,解题的关键是正确分析三角形各部分之间的关系.

 如图,直线m∥n,BA⊥AC于A点,AB、AC分别交直线n于点B、C,∠2=55°,则∠1的度数是( )
如图,直线m∥n,BA⊥AC于A点,AB、AC分别交直线n于点B、C,∠2=55°,则∠1的度数是( )| A. | 50° | B. | 45° | C. | 35° | D. | 30° |
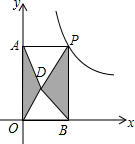 如图,点P是反比例函数y=$\frac{6}{x}$(x>0)的图象上的任意一点,过点P分别作两坐标轴的垂线,与坐标轴构成矩形OAPB,点D是矩形OAPB内任意一点,连接DA、DB、DP、DO,则图中阴影部分的面积是( )
如图,点P是反比例函数y=$\frac{6}{x}$(x>0)的图象上的任意一点,过点P分别作两坐标轴的垂线,与坐标轴构成矩形OAPB,点D是矩形OAPB内任意一点,连接DA、DB、DP、DO,则图中阴影部分的面积是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4. |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |