题目内容
5.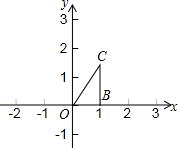 已知:如图,在平面直角坐标系xOy中,点B1、点C1的坐标分别为(1,0),(1,$\sqrt{3}$).将△OB1C1绕原点O逆时针旋转60°,再将其各边都扩大为原来的m倍,使OB2=OC1,得到△OB2C2,将△OB2C2绕原点O逆时针旋转60°,再将其各边都扩大为原来的m倍,使OB3=OC2,得到△OB3C3,如此下去,得到△OBnCn.
已知:如图,在平面直角坐标系xOy中,点B1、点C1的坐标分别为(1,0),(1,$\sqrt{3}$).将△OB1C1绕原点O逆时针旋转60°,再将其各边都扩大为原来的m倍,使OB2=OC1,得到△OB2C2,将△OB2C2绕原点O逆时针旋转60°,再将其各边都扩大为原来的m倍,使OB3=OC2,得到△OB3C3,如此下去,得到△OBnCn.(1)m的值是2;
(2)△OB2011C2011中,点C2011的坐标:(22010,22010$\sqrt{3}$).
分析 (1)易得OB2=mOB1=OC1,根据最初的三角形中OB1,OC1的关系可得m的值;
(2)可得旋转6次后,正好旋转一周,那么可得点C2011的坐标跟C1的坐标在一条射线上,其横纵坐标均为原来的2010倍.
解答 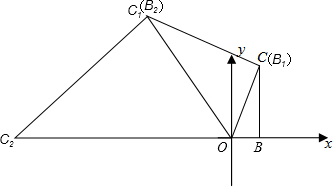 解:(1)在△OB1C1中,
解:(1)在△OB1C1中,
∵OB1=1,B1C1=$\sqrt{3}$,
∴tan∠C1OB1=$\sqrt{3}$,
∴∠C1OB1=60°,OC1=2,
∵OB2=mOB1,OB2=OC1,
∴m=2,
故答案为2;
(2)∵每一次的旋转角是60°,
∴旋转6次后C在x轴正半轴上,
∴2011÷6=335…1,
∴点C2011的坐标跟C1的坐标在一条射线上,
∵第2次旋转后,各边长是原来的2倍,第3次旋转后,各边长是原来的22倍,
∴点C2011的横纵坐标均为原来的2010倍.
故答案为:(22010,22010$\sqrt{3}$).
点评 本题考查了坐标与图形的变化-旋转,解直角三角形,根据解直角三角形,以及30°角所对的直角边等于斜边的一半,求出m的值是解题的关键.

练习册系列答案
相关题目
14.有一满池水,池底有泉水总能均匀地向外漏流,已知用24部A型抽水机,6天可抽干池水;若用21部A型抽水机8天也可抽干池水.设每部抽水机单位时间的抽水量相同,要使这一池水永远抽不干,则至多只能用( )部A型抽水机抽水.
| A. | 13 | B. | 12 | C. | 11 | D. | 10 |
20.小亮在匀速行驶的汽车里,注意到公路里程碑上的数如下:
则12:00时看到的两位数是27.
| 时刻 | 12:00 | 13:00 | 16:00 |
| 碑上的数 | 是一个两位数 | 十位与个位数字与12:00时 所看到的正好颠倒了 | 比12:00时看到的两位数 中间多了个0 |
17.下列四个多项式,哪一个是2x2+4x+2的因式?( )
| A. | 2x-1 | B. | 2x-3 | C. | x+1 | D. | x-3 |
 如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D.若AB=10,S△ABD=15,求CD的长.
如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D.若AB=10,S△ABD=15,求CD的长.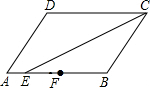 如图,在?ABCD中,CE平分∠DCB,F是AB的中点,AB=8,BC=6,则AE:EF:FB=1:1:2.
如图,在?ABCD中,CE平分∠DCB,F是AB的中点,AB=8,BC=6,则AE:EF:FB=1:1:2.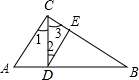 如图,在Rt△ABC中,AC⊥BC,CD⊥AB,∠1=∠2,有下列结论:(1)AC∥DE;(2)∠A=∠3;(3)∠B=∠1;(4)∠B与∠2互余;(5)∠A=∠2.其中正确的有(1)(2)(3)(填写所有正确的序号).
如图,在Rt△ABC中,AC⊥BC,CD⊥AB,∠1=∠2,有下列结论:(1)AC∥DE;(2)∠A=∠3;(3)∠B=∠1;(4)∠B与∠2互余;(5)∠A=∠2.其中正确的有(1)(2)(3)(填写所有正确的序号). 如图,在平行四边形ABCD中,CE平分∠BCD交AD边于点E,且DE=3,则AB的长为( )
如图,在平行四边形ABCD中,CE平分∠BCD交AD边于点E,且DE=3,则AB的长为( )