题目内容
13. 如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D.若AB=10,S△ABD=15,求CD的长.
如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D.若AB=10,S△ABD=15,求CD的长.
分析 过点D作DE⊥AB于E,根据角平分线上的点到角的两边距离相等可得DE=CD,然后利用△ABD的面积列式计算即可得解.
解答  解:如图,过点D作DE⊥AB于E,
解:如图,过点D作DE⊥AB于E,
∵∠C=90°,AD平分∠BAC,
∴DE=CD,
∴S△ABD=$\frac{1}{2}$AB•DE=$\frac{1}{2}$×10•DE=15,
解得DE=3,
∴CD=3.
点评 本题考查了角平分线上的点到角的两边距离相等的性质,三角形的面积,熟记性质是解题的关键.

练习册系列答案
相关题目
2.我县举行了一次艺术比赛,各年级组的参赛人数如下表所示:
(1)求全体参赛选手年龄的众数,中位数.
(2)王涛说,他所在年龄组的参赛人数占全体参赛人数的24%,你认为王涛是哪个年龄组的选手?请说明理由.
| 年龄组 | 13岁 | 14岁 | 15岁 | 16岁 |
| 参赛人数 | 5 | 19 | 12 | 14 |
(2)王涛说,他所在年龄组的参赛人数占全体参赛人数的24%,你认为王涛是哪个年龄组的选手?请说明理由.
8.下列三个长度的线段能组成直角三角形的是( )
| A. | 2,4,6 | B. | 1,$\sqrt{3}$,$\sqrt{5}$ | C. | 1,$\sqrt{2}$,$\sqrt{3}$ | D. | 5,5,6 |
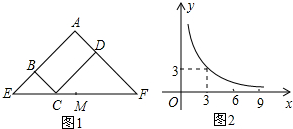
 如图,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=2.5cm,则AB的长为5cm.
如图,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=2.5cm,则AB的长为5cm.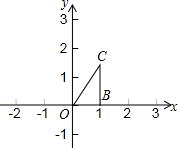 已知:如图,在平面直角坐标系xOy中,点B1、点C1的坐标分别为(1,0),(1,$\sqrt{3}$).将△OB1C1绕原点O逆时针旋转60°,再将其各边都扩大为原来的m倍,使OB2=OC1,得到△OB2C2,将△OB2C2绕原点O逆时针旋转60°,再将其各边都扩大为原来的m倍,使OB3=OC2,得到△OB3C3,如此下去,得到△OBnCn.
已知:如图,在平面直角坐标系xOy中,点B1、点C1的坐标分别为(1,0),(1,$\sqrt{3}$).将△OB1C1绕原点O逆时针旋转60°,再将其各边都扩大为原来的m倍,使OB2=OC1,得到△OB2C2,将△OB2C2绕原点O逆时针旋转60°,再将其各边都扩大为原来的m倍,使OB3=OC2,得到△OB3C3,如此下去,得到△OBnCn.