题目内容
10.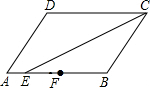 如图,在?ABCD中,CE平分∠DCB,F是AB的中点,AB=8,BC=6,则AE:EF:FB=1:1:2.
如图,在?ABCD中,CE平分∠DCB,F是AB的中点,AB=8,BC=6,则AE:EF:FB=1:1:2.
分析 根据题意可知,∠DCE=∠BEC=∠BCE,所以BE=BC=6,则AE=AB-BE=8-6=2,EF=AF-AE=4-2=2,又因为FB=AF=4,所以AE:EF:FB=1:1:2.
解答 解:∵四边形ABCD是平行四边形,
∴∠DCE=∠BEC,
∵CE是∠DCB的平分线,
∴∠DCE=∠BCE,
∴∠CEB=∠BCE,
∴BC=BE=6,
∵F是AB的中点,AB=8,
∴FB=4,
∴EF=BE-FB=2,
∴AE=AB-EF-FB=2,
∴AE:EF:FB=1:1:2,
故答案为1:1:2.
点评 本题主要考查了平行四边形的性质,在平行四边形中,当出现角平分线时,一般可构造等腰三角形,进而利用等腰三角形的性质解题.

练习册系列答案
相关题目
20.甲乙两厂分别有肥料240吨,300吨.现要把这些肥料全部运往A,B两地,从甲厂往A地,B地的运费分别是每吨20元和30元,从乙厂运往A地,B地的运费分别是每吨23元和15元,现A地需要260吨,B地要280吨.设:甲厂运往A地的化肥为x吨.
(1)完成下表
(2)设调运总费用为y元,则如何调运可使总运费y最少?
(1)完成下表
| 厂家 数据 地点 | 甲厂(240吨) | 乙厂(300吨) |
| A地(260吨) | x吨 | 260-x |
| B地(280吨) | 240-x | 40+x |
 如图,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=2.5cm,则AB的长为5cm.
如图,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=2.5cm,则AB的长为5cm.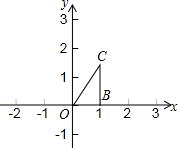 已知:如图,在平面直角坐标系xOy中,点B1、点C1的坐标分别为(1,0),(1,$\sqrt{3}$).将△OB1C1绕原点O逆时针旋转60°,再将其各边都扩大为原来的m倍,使OB2=OC1,得到△OB2C2,将△OB2C2绕原点O逆时针旋转60°,再将其各边都扩大为原来的m倍,使OB3=OC2,得到△OB3C3,如此下去,得到△OBnCn.
已知:如图,在平面直角坐标系xOy中,点B1、点C1的坐标分别为(1,0),(1,$\sqrt{3}$).将△OB1C1绕原点O逆时针旋转60°,再将其各边都扩大为原来的m倍,使OB2=OC1,得到△OB2C2,将△OB2C2绕原点O逆时针旋转60°,再将其各边都扩大为原来的m倍,使OB3=OC2,得到△OB3C3,如此下去,得到△OBnCn.