题目内容
4.在菱形ABCD中,∠BAD=120°,AC=$\sqrt{3}$,则菱形的周长等于4$\sqrt{3}$.分析 由于四边形ABCD是菱形,AC是对角线,根据菱形对角线性质可求∠BAC=60°,而AB=BC,易证△BAC是等边三角形,从而可求AB=BC=3,即AB=BC=CD=AD=3,那么就可求菱形的周长.
解答 解:如图所示,
∵四边形ABCD是菱形,AC是对角线,
∴AB=BC=CD=AD,∠BAC=∠CAD=$\frac{1}{2}$∠BAD,
∴∠BAC=60°,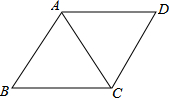
∴△ABC是等边三角形,
∴AB=BC=AC=$\sqrt{3}$,
∴AB=BC=CD=AD=$\sqrt{3}$,
∴菱形ABCD的周长是4$\sqrt{3}$.
故答案为:4$\sqrt{3}$.
点评 本题考查了菱形的性质、等边三角形的判定和性质.菱形的对角线平分对角,解题的关键是证明△ABC是等边三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.已知二元一次方程x+y=1,下列说法不正确的是( )
| A. | 它有无数多组解 | B. | 它只有一组非负整数解 | ||
| C. | 它有无数多组整数解 | D. | 它没有正整数解 |
19.二次函数y=ax2+bx+1(a>1)的图象与x轴两个交点的横坐标分别为x1,x2(x1<x2),一元二次方程a2x2+bx+1=0有两个实数根x3,x4(x3<x4),则x1,x2,x3,x4的大小关系是( )
| A. | x1<x2<x3<x4 | B. | x1<x3<x4<x2 | C. | x3<x1<x2<x4 | D. | x3<x4<x1<x2 |
9.方程$\frac{x+1}{2}-\frac{x}{4}=1$的解为( )
| A. | x=-1 | B. | x=0 | C. | x=1 | D. | x=2 |
16. 第1个正方形A1B1C1O,第2个正方形A2B2C2C1,第3个正方形A3B3C3C2,…按如图所示方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则第n个正方形的边长为( )
第1个正方形A1B1C1O,第2个正方形A2B2C2C1,第3个正方形A3B3C3C2,…按如图所示方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则第n个正方形的边长为( )
 第1个正方形A1B1C1O,第2个正方形A2B2C2C1,第3个正方形A3B3C3C2,…按如图所示方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则第n个正方形的边长为( )
第1个正方形A1B1C1O,第2个正方形A2B2C2C1,第3个正方形A3B3C3C2,…按如图所示方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则第n个正方形的边长为( )| A. | n | B. | 2n-1 | C. | 2n-1 | D. | 2n-1 |
14.已知ab≠0,方程ax2+bx+c=0的系数满足($\frac{b}{2}$)2=ac,则方程的两根之比为( )
| A. | 0:1 | B. | 1:1 | C. | 1:2 | D. | 2:3 |

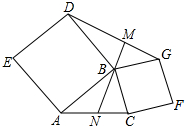 若以△ABC的边AB,BC为边向三角形外作正方形ABDE,BCFG,N为AC中点,求证:DG=2BN,BM⊥DG.
若以△ABC的边AB,BC为边向三角形外作正方形ABDE,BCFG,N为AC中点,求证:DG=2BN,BM⊥DG.