题目内容
3.已知平面直角坐标系内有一半径为10$\sqrt{3}$的圆,其圆心O点与坐标原点重合,P(a,b)、Q(m,n)为圆上两点(P、Q不重合),已知a、b、m、n满足方程$\left\{\begin{array}{l}{a+b+m+n=4\sqrt{3}}\\{a+b-m-n=0}\end{array}\right.$.求直线PQ的解析式.分析 由方程组可得a+b=2$\sqrt{3}$即b=2$\sqrt{3}$-a、m+n=2$\sqrt{3}$即n=2$\sqrt{3}$-m,从而得出点P(a,2$\sqrt{3}$-a)、Q(m,2$\sqrt{3}$-m),将其代入y=kx+b求出k、b的值即可得.
解答 解:由方程组$\left\{\begin{array}{l}{a+b+m+n=4\sqrt{3}}&{①}\\{a+b-m-n=0}&{②}\end{array}\right.$,
①+②,得:a+b=2$\sqrt{3}$,即b=2$\sqrt{3}$-a,
①-②,得:m+n=2$\sqrt{3}$,即n=2$\sqrt{3}$-m,
则点P(a,2$\sqrt{3}$-a)、Q(m,2$\sqrt{3}$-m),
设直线解析式为y=kx+b,
将点P、Q代入,得:$\left\{\begin{array}{l}{ak+b=2\sqrt{3}-a}\\{mk+b=2\sqrt{3}-m}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=2\sqrt{3}}\end{array}\right.$,
∴直线PQ的解析式为y=-x+2$\sqrt{3}$.
点评 本题主要考查待定系数法求一次函数解析式,熟练掌握待定系数法是解题的根本.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,抛物线m:y=$\frac{1}{2}$x2平移得到抛物线n,抛物线m与x轴交于点O,点A.若它的顶点坐标为P(-3,-$\frac{9}{2}$),它的对称轴与抛物线y=$\frac{1}{2}$x2交于点O.
如图,抛物线m:y=$\frac{1}{2}$x2平移得到抛物线n,抛物线m与x轴交于点O,点A.若它的顶点坐标为P(-3,-$\frac{9}{2}$),它的对称轴与抛物线y=$\frac{1}{2}$x2交于点O. 如图,在Rt△ABC中,∠ACB=90°,AC=2,BC=2$\sqrt{3}$,D为线段AC上一点,△DEF是边长为a(a为小于2$\sqrt{3}$的常数)的等边三角形,且DE∥AB,将△DEF沿AC方向上下平移,设△DEF与△ABC重叠部分的周长为L.
如图,在Rt△ABC中,∠ACB=90°,AC=2,BC=2$\sqrt{3}$,D为线段AC上一点,△DEF是边长为a(a为小于2$\sqrt{3}$的常数)的等边三角形,且DE∥AB,将△DEF沿AC方向上下平移,设△DEF与△ABC重叠部分的周长为L.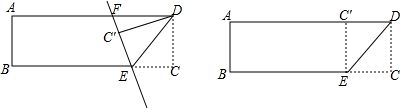
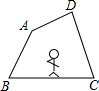 如图,小明沿画在地面上的四边形ABCD的边逆时针走一圈回到原地.
如图,小明沿画在地面上的四边形ABCD的边逆时针走一圈回到原地.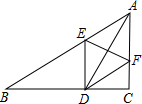 如图,△ABC中,∠C=90°,AD平分∠BAC,ED⊥BC,DF∥AB,求证:AD与EF互相垂直平分.
如图,△ABC中,∠C=90°,AD平分∠BAC,ED⊥BC,DF∥AB,求证:AD与EF互相垂直平分.