题目内容
13.阅读下列材料,然后解答下列问题:在进行代数式化简时,我们有时会碰上如$\frac{5}{\sqrt{3}}$,$\frac{2}{\sqrt{3}+1}$这样的式子,其实我们还可以将其进一步化简:(一)$\frac{5}{\sqrt{3}}$=$\frac{5×\sqrt{3}}{\sqrt{3}×\sqrt{3}}$=$\frac{5}{3}$$\sqrt{3}$;
(二)$\frac{2}{\sqrt{3}+1}$=$\frac{2×(\sqrt{3}-1)}{(\sqrt{3}+1)(\sqrt{3}-1)}$=$\frac{2(\sqrt{3}-1)}{(\sqrt{3})^{2}-1}$=$\sqrt{3}$-1;
(三)$\frac{2}{\sqrt{3}+1}$=$\frac{3-1}{\sqrt{3}+1}$=$\frac{(\sqrt{3})^{2}-{1}^{2}}{\sqrt{3}+1}$=$\frac{(\sqrt{3}+1)(\sqrt{3}-1)}{\sqrt{3}+1}$=$\sqrt{3}$-1.以上这种化简的方法叫分母有理化.
(1)请用不同的方法化简$\frac{2}{\sqrt{5}+\sqrt{3}}$:
①参照(二)式化简$\frac{2}{\sqrt{5}+\sqrt{3}}$=$\sqrt{5}$-$\sqrt{3}$.
②参照(三)式化简$\frac{2}{\sqrt{5}+\sqrt{3}}$=$\sqrt{5}$-$\sqrt{3}$.
(2)化简:$\frac{1}{\sqrt{3}+1}$+$\frac{1}{\sqrt{5}+\sqrt{3}}$+$\frac{1}{\sqrt{7}+\sqrt{5}}$+…+$\frac{1}{\sqrt{99}+\sqrt{97}}$.
分析 (1)原式各项仿照题中分母有理化的方法计算即可得到结果;
(2)原式各项分母有理化,计算即可得到结果.
解答 解:(1)①$\frac{2×(\sqrt{5}-\sqrt{3})}{(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})}$=$\frac{2(\sqrt{5}-\sqrt{3})}{(\sqrt{5})2-(\sqrt{3})2}$=$\sqrt{5}$-$\sqrt{3}$;
②$\frac{5-3}{\sqrt{5}+\sqrt{3}}$=$\frac{(\sqrt{5})^{2}-(\sqrt{3})^{2}}{\sqrt{5}+\sqrt{3}}$=$\frac{(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})}{\sqrt{5}+\sqrt{3}}$=$\sqrt{5}$-$\sqrt{3}$;
(2)原式=$\frac{\sqrt{3}-1}{2}$+$\frac{\sqrt{5}-\sqrt{3}}{2}$+$\frac{\sqrt{7}-\sqrt{5}}{2}$+…+$\frac{\sqrt{99}-\sqrt{97}}{2}$=$\frac{\sqrt{99}-1}{2}$=$\frac{3\sqrt{11}-1}{2}$.
故答案为:(1)①$\sqrt{5}$-$\sqrt{3}$;②$\sqrt{5}$-$\sqrt{3}$
点评 此题考查了分母有理化,熟练掌握分母有理化的方法是解本题的关键.

练习册系列答案
相关题目
8.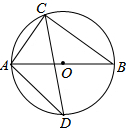 如图,已知AB是⊙O的直径,C点在⊙O上,CD平分∠ACB,若AC=6,BC=8,则AD长为( )
如图,已知AB是⊙O的直径,C点在⊙O上,CD平分∠ACB,若AC=6,BC=8,则AD长为( )
 如图,已知AB是⊙O的直径,C点在⊙O上,CD平分∠ACB,若AC=6,BC=8,则AD长为( )
如图,已知AB是⊙O的直径,C点在⊙O上,CD平分∠ACB,若AC=6,BC=8,则AD长为( )| A. | $\frac{4}{3}$ | B. | 5 | C. | 5$\sqrt{3}$ | D. | 5$\sqrt{2}$ |
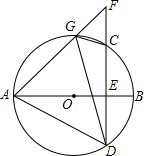 如图,AB是圆O的直径,弦CD⊥AB于点E,G是$\widehat{AC}$上任意一点,连结AD,GD,GC,延长AG、DC交于点F.
如图,AB是圆O的直径,弦CD⊥AB于点E,G是$\widehat{AC}$上任意一点,连结AD,GD,GC,延长AG、DC交于点F. 如图,抛物线y=ax2+bx+c经过A(-3,0)、B(1,0)、C(0,-3)三点.
如图,抛物线y=ax2+bx+c经过A(-3,0)、B(1,0)、C(0,-3)三点.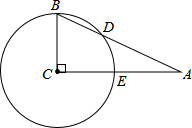 如图,在△ABC中,∠C=90°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E.
如图,在△ABC中,∠C=90°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E.