题目内容
2. 如图,抛物线m:y=$\frac{1}{2}$x2平移得到抛物线n,抛物线m与x轴交于点O,点A.若它的顶点坐标为P(-3,-$\frac{9}{2}$),它的对称轴与抛物线y=$\frac{1}{2}$x2交于点O.
如图,抛物线m:y=$\frac{1}{2}$x2平移得到抛物线n,抛物线m与x轴交于点O,点A.若它的顶点坐标为P(-3,-$\frac{9}{2}$),它的对称轴与抛物线y=$\frac{1}{2}$x2交于点O.(1)写出抛物线n的解析式;
(2)写出把抛物线m平移到抛物线n的平移过程;
(3)求出点A,点O,点Q的坐标;
(4)写出图中阴影部分的面积.
分析 (1)利用成顶点式即可解决问题;
(2)利用顶点的平移过程得到抛物线的平移过程;
(3)根据平移得到图中阴影部分的面积=S△OPQ,求出PQ、OM,然后根据三角形面积公式计算;
解答 解:(1)∵平移的后抛物线的顶点为P(-3,-$\frac{9}{2}$),
∴解析式为y=$\frac{1}{2}$(x+3)2-$\frac{9}{2}$.
(2)∵原抛物线顶点(0,0),平移后的抛物线顶点为P(-3,-$\frac{9}{2}$),
∴y=$\frac{1}{2}$x2先向左平移3个单位,再向下平移 $\frac{9}{2}$个单位即可得到抛物线y=$\frac{1}{2}$(x+3)2-$\frac{9}{2}$;
(3)∵PQ∥y轴,P(-3,-$\frac{9}{2}$),
∴Q(-3,$\frac{9}{2}$),
∴PQ=9,OM=3,
图中阴影部分的面积=S△OPQ=$\frac{1}{2}$×3×9=$\frac{27}{2}$.
点评 本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.设一元二次方程(x-2)(x-3)=m(m>0)的两实根分别为α、β(α<β),则α、β满足( )
| A. | 2<α<β<3 | B. | 2<α<3<β | C. | α<2<β<3 | D. | α<2且β>3 |
 如图,在⊙O中,弦AB、DC的延长线交于点E,且DC=CE,C是$\widehat{BD}$的中点.求证:AD是⊙O的直径.
如图,在⊙O中,弦AB、DC的延长线交于点E,且DC=CE,C是$\widehat{BD}$的中点.求证:AD是⊙O的直径. 如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,且AB+BC=18厘米,若要求出CD和AC的长,还需要添加什么条件?
如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为点D,且AB+BC=18厘米,若要求出CD和AC的长,还需要添加什么条件?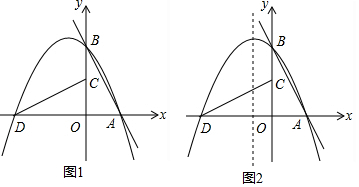
 如图,在△ABC中,BD平分∠ABC的交AC于点D,DE∥BC交AB于点E,∠A=60°,∠BDC=100°,求△BDE各个内角的度数.
如图,在△ABC中,BD平分∠ABC的交AC于点D,DE∥BC交AB于点E,∠A=60°,∠BDC=100°,求△BDE各个内角的度数.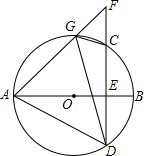 如图,AB是圆O的直径,弦CD⊥AB于点E,G是$\widehat{AC}$上任意一点,连结AD,GD,GC,延长AG、DC交于点F.
如图,AB是圆O的直径,弦CD⊥AB于点E,G是$\widehat{AC}$上任意一点,连结AD,GD,GC,延长AG、DC交于点F.