题目内容
6.己知:一张矩形纸片记作矩形ABCD,CD=3,AD=8,点E是边BC上的点,连结DE,将△DEC沿着DE所在的直线折叠,记点C的对称点为点C′,C′E所在的直线交边AD于点F,设EC=x.(1)若点C′恰好落在边AD上,求x的值.
(2)①若点C′落在矩形ABCD内部,求证:△FED是等腰三角形.
②当△FED是等边三角形时,x=$\sqrt{3}$(直接写出答案)
(3)当x=6时,△FED的面积=$\frac{45}{8}$(直接写出答案)
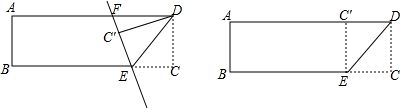
分析 (1)只要证明△EDC是等腰三角形即可.
(2)①欲证明△DEF是等腰三角形,只要证明∠FED=∠FDE即可.
②在Rt△DEC中,根据EC=DC•tan30°即可解决问题.
(3)如图4中,作EM⊥AD于M.设FE=FD=x,在Rt△DEM中,∵FM=DM-DF=EC-DF=6-x,EM=CD=3,利用勾股定理列出方程即可.
解答 解:(1)如图1中,
点C′恰好落在边AD上时,
∵四边形ABCD是矩形,
∴∠C=∠ADC=90°,
由折叠的性质可知∠EDC=∠EDF=45°,
∵∠C=∠EC′D=90°,
∴△DEC′,△DEC都是等腰直角三角形,
∴x=EC=CD=3,
(2)①如图2中,
点C′落在矩形ABCD内部时,∵∠DEC=∠DEC′,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠FDE=∠DEC,
∴∠FED=∠FDE,
∴FE=FD,
∴△DEF是等腰三角形.
②如图3,
∵△DEF是等边三角形,
∴∠FDE=60°,
∴∠EDC=90°-∠FDE=30°,
在Rt△DEC中,EC=DC•tan30°=3×$\frac{\sqrt{3}}{3}$=$\sqrt{3}$.
∴x=$\sqrt{3}$,
故答案为$\sqrt{3}$.
(3)如图4中,作EM⊥AD于M.
∵∠CED=∠DEF=∠FDE,
∴FE=FD,设FE=FD=x,
在Rt△DEM中,∵FM=DM-DF=EC-DF=6-x,EM=CD=3,
∴32+(6-x)2=x2,
∴x=$\frac{15}{4}$,
∴EF=$\frac{15}{4}$,
∴S△EFD=$\frac{1}{2}$•EF•DC′=$\frac{1}{2}$×$\frac{15}{4}$×3=$\frac{45}{8}$.
故答案为$\frac{45}{8}$.
点评 本题考查四边形综合题、矩形的性质、等边三角形的性质、翻折变换等知识,解题的关键是灵活运用这些知识解决问题,学会用方程的思想思考问题,属于中考压轴题.

 金钥匙试卷系列答案
金钥匙试卷系列答案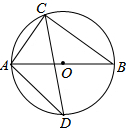 如图,已知AB是⊙O的直径,C点在⊙O上,CD平分∠ACB,若AC=6,BC=8,则AD长为( )
如图,已知AB是⊙O的直径,C点在⊙O上,CD平分∠ACB,若AC=6,BC=8,则AD长为( )| A. | $\frac{4}{3}$ | B. | 5 | C. | 5$\sqrt{3}$ | D. | 5$\sqrt{2}$ |
 如图所示,AD,BE分别是△ABC中BC,AC边上的中线,AD与BE相交于点O,连接DE,若S△DOE=2,求S△AOB和S△ABC.
如图所示,AD,BE分别是△ABC中BC,AC边上的中线,AD与BE相交于点O,连接DE,若S△DOE=2,求S△AOB和S△ABC.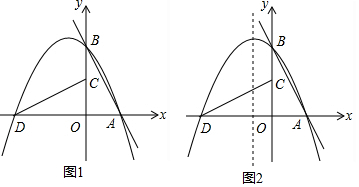
 如图,在△ABC中,BD平分∠ABC的交AC于点D,DE∥BC交AB于点E,∠A=60°,∠BDC=100°,求△BDE各个内角的度数.
如图,在△ABC中,BD平分∠ABC的交AC于点D,DE∥BC交AB于点E,∠A=60°,∠BDC=100°,求△BDE各个内角的度数.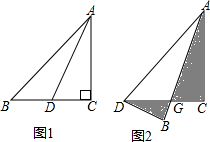 如图①,已知等腰直角三角形ABC,沿着直角边上的中线AD按图②所示折叠,设AB与DC相交于点G,问:△AGC和△BGD的面积哪个大?为什么?
如图①,已知等腰直角三角形ABC,沿着直角边上的中线AD按图②所示折叠,设AB与DC相交于点G,问:△AGC和△BGD的面积哪个大?为什么?