Question

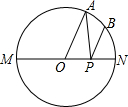如图，MN是⊙O的直径，MN=2，点A在⊙O上，

AN

的度数为60°，点B为

AN

的中点，P是直径MN上的一个动点，求PA+PB的最小值．

Answer 1

考点：轴对称-最短路线问题,勾股定理,垂径定理

专题：

分析：要在MN上找一点P，使PA+PB的值最小，设A′是A关于MN的对称点，连接A′B，与MN的交点即为点P．此时PA+PB=A′B是最小值，可证△OA′B是等腰直角三角形，从而得出结果．

解答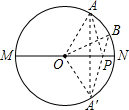：解：作点A关于MN的对称点A′，连接A′B，交MN于点P，连接OA′，OA，OB，PA，AA′．
∵点A与A′关于MN对称，点A是半圆上的一个三等分点，
∴∠A′ON=∠AON=60°，PA=PA′，
∵点B是弧AN的中点，
∴∠BON=30°，
∴∠A′OB=∠A′ON+∠BON=90°，
又∵OA=OA′=1，
∴A′B=

2

．
∴PA+PB=PA′+PB=A′B=

2

．

点评：本题考查的是轴对称--最短路线问题．其中求出∠BOA′的度数是解题的关键．