题目内容
a是不为1的有理数,我们把
称为a的差倒数.如:2的差倒数是
=-1,-1的差倒数是
=
.已知a1=-
,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…,依此类推,则a2013=( )
| 1 |
| 1-a |
| 1 |
| 1-2 |
| 1 |
| 1-(-1) |
| 1 |
| 2 |
| 1 |
| 3 |
A、-
| ||
B、
| ||
| C、4 | ||
| D、2013 |
考点:规律型:数字的变化类,倒数
专题:
分析:由已知,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数,…,则a2=
,a3=
,a4=
,…,把a1=-
代入求出a2的值,用同样的方法分别求出a3,a4,…的值,从中找出规律.
| 1 |
| 1-a1 |
| 1 |
| 1-a2 |
| 1 |
| 1-a3 |
| 1 |
| 3 |
解答:解:由已知,a1=-
,
a2=
=
,
a3=
=4,
a4=
=-
,
…
得出-
,
,4这3个数一循环,
2013÷3=671.
所以a2013=a3=4.
故选:C.
| 1 |
| 3 |
a2=
| 1 | ||
1-(-
|
| 3 |
| 4 |
a3=
| 1 | ||
1-
|
a4=
| 1 |
| 1-4 |
| 1 |
| 3 |
…
得出-
| 1 |
| 3 |
| 3 |
| 4 |
2013÷3=671.
所以a2013=a3=4.
故选:C.
点评:此题考查了数字的变化规律,解答问题的关键是由已知先计算出前面几个数找出规律.

练习册系列答案
相关题目
 某物体从不同方向看到的三种形状图如图所示,那么该物体的形状是( )
某物体从不同方向看到的三种形状图如图所示,那么该物体的形状是( )| A、长方体 | B、圆锥体 |
| C、立方体 | D、圆柱体 |
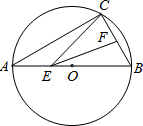 如图,AB是⊙O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°.若动点E从A点出发沿着A→B方向运动,连接EF、CE,则EF+CE最小值是
如图,AB是⊙O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°.若动点E从A点出发沿着A→B方向运动,连接EF、CE,则EF+CE最小值是
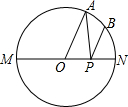 如图,MN是⊙O的直径,MN=2,点A在⊙O上,
如图,MN是⊙O的直径,MN=2,点A在⊙O上,