题目内容
 如图,在平面直角坐标系xOy中,矩形ABCD的边AB在x轴上,且AB=3,BC=4,直线y=2x-4经过点C,交y轴于点G.
如图,在平面直角坐标系xOy中,矩形ABCD的边AB在x轴上,且AB=3,BC=4,直线y=2x-4经过点C,交y轴于点G.(1)点C、D的坐标分别是C (
(2)求顶点在直线y=2x-4上且经过点C、D的抛物线的解析式;
(3)将(2)中的抛物线沿直线y=2x-4平移,平移后的抛物线交y轴于点F,顶点为点E.平移后是否存在这样的抛物线,使△EFG为等腰三角形?若存在,请求出此时抛物线顶点E的坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)由BC=4就可以得出C点的纵坐标为4,将y=4代入解析式y=2x-4求出x的值就可以求出B的坐标及C的坐标,同时可以得出OB的值,由AB=3就可以求出OA的值,而得出D的坐标;
(2)由C、D的纵坐标相等就可以求出抛物线的对称轴,由顶点在直线GC上就可以求出顶点坐标,再由待定系数法就可以求出抛物线的解析式;
(3)根据抛物线沿直线y=2x-4平移,设抛物线的顶点坐标为(m,2m-4),则抛物线的解析式为y=
(x-m)2+2m-4.分情况.当m>0时,如图1,当EF=EG时,由两点间的距离公式可以得出EF=EG=
m,OH=4-2m,HG=2m,OF=4m-4,F的坐标为(0,4m-4),代入解析式就可以求出结论;如图2,GE=GF时,得出GE=GF=
m,OF=4-
m,F(0,
m-4),代入解析式就可以求出结论;当m<0时,如图3,GE=GF时,得出GE=GF=-
m,OF=-4-
m,F(0,-
m-4),代入解析式就可以求出结论;当EF=EG时不存在.
(2)由C、D的纵坐标相等就可以求出抛物线的对称轴,由顶点在直线GC上就可以求出顶点坐标,再由待定系数法就可以求出抛物线的解析式;
(3)根据抛物线沿直线y=2x-4平移,设抛物线的顶点坐标为(m,2m-4),则抛物线的解析式为y=
| 4 |
| 3 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
解答:解:(1)∵四边形ABCD是矩形,
∴AD=BC,AB=CD,CD∥AB,AD⊥AB,BC⊥AB.
∵BC=4,
∴C的纵坐标为4,AD=3.
∴4=2x-4,
∴x=4,
∴C(4,4),
∴OB=4.
∵AB=3,
∴OA=1,
∴(1,4)
故答案为:C(4,4)D(1,4);
(2)∵CD∥x轴,C(4,4)D(1,4);
∴抛物线的对称轴为:x=
=2.5,
∴y=2×2.5-4=1,
∴顶点坐标为(2.5,1).
设抛物线的解析式为:y=a(x-2.5)2+1,由题意,得
4=a(4-2.5)2+1,
解得:a=
,
∴抛物线的解析式为:y=
(x-
)2+1;
(3)∵抛物线的顶点在直线y=2x-4上平移,设顶点作表为(m,2m-4),
∴抛物线的解析式为y=
(x-m)2+2m-4.
当m>0时,如图1,当EF=EG时,作EH⊥y轴,
FH=GH.
∴OH=4-2m,
∴HG=4-(4-2m)=2m,
∴OF=2m-(4-2m)=4m-4,
∴F(0,4m-4),
∴4m-4=
(0-m)2+2m-4,
解得:m1=0(舍去),m2=
;
∴2m-4=-1,
∴E(
,-1);
如图2,GE=GF时,得出GE=GF=
=
m.
∵OG=4,
∴OF=4-
m,
∴F(0,
m-4),
∴
m-4=
(0-m)2+2m-4,
∴m1=0(舍去),m2=
,
∴2m-4=
,
∴E(
,
);
当m<0时,如图3,GE=GF时,得出GE=GF=
=-
m,
∵OG=4,
∴OF=-
m-4,
∴F(0,-
m-4),
∴-
m-4=
(0-m)2+2m-4,
∴m1=0,m2=
,
∴2m-4=
,
∴E(
,
).
当EF=EG时不存在.
∴E的坐标为:(
,-1);(
,
);(
,
).
∴AD=BC,AB=CD,CD∥AB,AD⊥AB,BC⊥AB.
∵BC=4,
∴C的纵坐标为4,AD=3.
∴4=2x-4,
∴x=4,
∴C(4,4),
∴OB=4.
∵AB=3,
∴OA=1,
∴(1,4)
故答案为:C(4,4)D(1,4);
(2)∵CD∥x轴,C(4,4)D(1,4);

∴抛物线的对称轴为:x=
| 4+1 |
| 2 |
∴y=2×2.5-4=1,
∴顶点坐标为(2.5,1).
设抛物线的解析式为:y=a(x-2.5)2+1,由题意,得
4=a(4-2.5)2+1,
解得:a=
| 4 |
| 3 |
∴抛物线的解析式为:y=
| 4 |
| 3 |
| 5 |
| 2 |
(3)∵抛物线的顶点在直线y=2x-4上平移,设顶点作表为(m,2m-4),
∴抛物线的解析式为y=
| 4 |
| 3 |
当m>0时,如图1,当EF=EG时,作EH⊥y轴,
FH=GH.
∴OH=4-2m,

∴HG=4-(4-2m)=2m,
∴OF=2m-(4-2m)=4m-4,
∴F(0,4m-4),
∴4m-4=
| 4 |
| 3 |
解得:m1=0(舍去),m2=
| 3 |
| 2 |
∴2m-4=-1,
∴E(
| 3 |
| 2 |
如图2,GE=GF时,得出GE=GF=
| (m-0)2+[2m-4-(-4)]2 |
| 5 |
∵OG=4,
∴OF=4-
| 5 |
∴F(0,
| 5 |
∴
| 5 |
| 4 |
| 3 |

∴m1=0(舍去),m2=
3
| ||
| 4 |
∴2m-4=
3
| ||
| 2 |
∴E(
3
| ||
| 4 |
3
| ||
| 2 |
当m<0时,如图3,GE=GF时,得出GE=GF=
| (m-0)2+[2m-4-(-4)]2 |
| 5 |
∵OG=4,
∴OF=-
| 5 |
∴F(0,-
| 5 |
∴-
| 5 |
| 4 |
| 3 |
∴m1=0,m2=
-6-3
| ||
| 4 |
∴2m-4=
-14-3
| ||
| 2 |
∴E(
-6-3
| ||
| 4 |
-14-3
| ||
| 2 |
当EF=EG时不存在.
∴E的坐标为:(
| 3 |
| 2 |
3
| ||
| 4 |
3
| ||
| 2 |
-6-3
| ||
| 4 |
-14-3
| ||
| 2 |
点评:本题考查了矩形的性质的运用,抛物线的性质和它的顶点式的运用,两点间的距离公式的运用,一次函数的性质和分类讨论思想的运用.解答时求出二次函数的解析式是关键.

练习册系列答案
相关题目
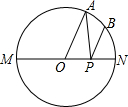 如图,MN是⊙O的直径,MN=2,点A在⊙O上,
如图,MN是⊙O的直径,MN=2,点A在⊙O上,
 如图A、B、C、D在同一直线上,BE⊥AD,CF⊥AD,垂足分别是B,C,AB=DC,AE=DF.求证:AF=DE.
如图A、B、C、D在同一直线上,BE⊥AD,CF⊥AD,垂足分别是B,C,AB=DC,AE=DF.求证:AF=DE.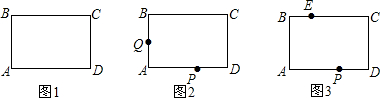
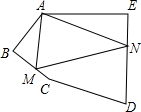 如图,在五边形ABCDE中,∠BAE=120°,∠B=∠E=90°,AB=BC,AE=DE,在边BC、DE上分别找一点M、N,使得△AMN周长最小,则∠AMN+∠ANM=
如图,在五边形ABCDE中,∠BAE=120°,∠B=∠E=90°,AB=BC,AE=DE,在边BC、DE上分别找一点M、N,使得△AMN周长最小,则∠AMN+∠ANM=