题目内容
在△ABC中,CA=CB=6,∠ACB=120°,将△ABC绕点C逆时针旋转角α(0°<α<120°)得△A1CB1,A1C交AB于E,A1B1分别交AB、CB于D、F,连结A1A.
(1)当α为多少度时,△AA1E是等腰三角形;
(2)当α=30°时,求DE的长.
(1)当α为多少度时,△AA1E是等腰三角形;
(2)当α=30°时,求DE的长.
考点:旋转的性质
专题:计算题
分析:(1)如图1,根据等腰三角形的性质和三角形内角和计算出∠CAB=30°,再根据旋转的性质得∠ACA1=α,CA=CA1,于是利用等腰三角形的性质和三角形内角和可计算得到∠CAA1=∠CA1A=90°-
α,则∠EAA1=∠CAA1-∠CAB=60°-
α,由三角形外角性质得∠AEA1=∠CAE+∠ACE=30°+α,然后分类讨论:当∠AEA1=∠AA1E时,△AA1E是等腰三角形,此时30°+α=90°-
α;当∠AEA1=∠EA1A时,△AA1E是等腰三角形,此时30°+α=60°-
α,再分别计算出α即可;
(2)作EH⊥AC于H,A1G⊥AE于G,如图2,先由(1)中的结论计算出∠EAA1=60°-
α=45°,∠AEA1=30°+α=60°,可判断△EAC为等腰三角形,则AH=CH=
AC=3,在Rt△AHE中,根据含30度的直角三角形三边的关系得HE=
AH=
,AE=2HE=2
;设GE=x,在Rt△A1GE中得到A1E=2GE=2x,A1G=
GE=
x,在Rt△AA1G中得到AG=A1G=
x,则
x+x=2
,解得x=3-
,然后证明ED=EA1即可.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)作EH⊥AC于H,A1G⊥AE于G,如图2,先由(1)中的结论计算出∠EAA1=60°-
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
解答:解:(1)如图1,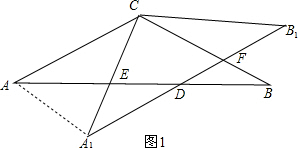
∵CA=CB=6,∠ACB=120°,
∴∠CAB=30°,
∵△ABC绕点C逆时针旋转角α(0°<α<120°)得△A1CB1,
∴∠ACA1=α,CA=CA1,
∴∠CAA1=∠CA1A=
(180°-∠ACA1)=90°-
α,
∴∠EAA1=∠CAA1-∠CAB=90°-
α-30°=60°-
α,
而∠AEA1=∠CAE+∠ACE=30°+α,
当∠AEA1=∠AA1E时,△AA1E是等腰三角形,此时30°+α=90°-
α,解得α=40°;
当∠AEA1=∠EA1A时,△AA1E是等腰三角形,此时30°+α=60°-
α,解得α=20°;
即α为20度或40度时,△AA1E是等腰三角形;
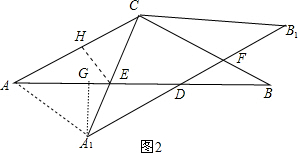 (2)作EH⊥AC于H,A1G⊥AE于G,如图2,
(2)作EH⊥AC于H,A1G⊥AE于G,如图2,
∵α=30°,即∠ACA1=30°,
∴∠EAA1=60°-
α=45°,∠AEA1=30°+α=60°,
∵∠CAB=∠ACA1=30°,
∴△EAC为等腰三角形,
∴AH=CH=
AC=3,
在Rt△AHE中,HE=
AH=
,AE=2HE=2
,
设GE=x,
在Rt△A1GE中,∵∠GEA1=30°+α=60°,
∴∠EA1G=30°,
∴A1E=2GE=2x,A1G=
GE=
x,
在Rt△AA1G中,∵∠GAA1=45°,
∴AG=A1G=
x,
∴
x+x=2
,解得x=3-
,
∴A1E=6-2
,
∵∠CA1B1=∠CAB=30°,
而∠AEA1=∠EA1D+∠EDA1=60°,
∴∠EDA1=30°,
∴ED=EA1=6-2
.

∵CA=CB=6,∠ACB=120°,
∴∠CAB=30°,
∵△ABC绕点C逆时针旋转角α(0°<α<120°)得△A1CB1,
∴∠ACA1=α,CA=CA1,
∴∠CAA1=∠CA1A=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠EAA1=∠CAA1-∠CAB=90°-
| 1 |
| 2 |
| 1 |
| 2 |
而∠AEA1=∠CAE+∠ACE=30°+α,
当∠AEA1=∠AA1E时,△AA1E是等腰三角形,此时30°+α=90°-
| 1 |
| 2 |
当∠AEA1=∠EA1A时,△AA1E是等腰三角形,此时30°+α=60°-
| 1 |
| 2 |
即α为20度或40度时,△AA1E是等腰三角形;
 (2)作EH⊥AC于H,A1G⊥AE于G,如图2,
(2)作EH⊥AC于H,A1G⊥AE于G,如图2,∵α=30°,即∠ACA1=30°,
∴∠EAA1=60°-
| 1 |
| 2 |
∵∠CAB=∠ACA1=30°,
∴△EAC为等腰三角形,
∴AH=CH=
| 1 |
| 2 |
在Rt△AHE中,HE=
| ||
| 3 |
| 3 |
| 3 |
设GE=x,
在Rt△A1GE中,∵∠GEA1=30°+α=60°,
∴∠EA1G=30°,
∴A1E=2GE=2x,A1G=
| 3 |
| 3 |
在Rt△AA1G中,∵∠GAA1=45°,
∴AG=A1G=
| 3 |
∴
| 3 |
| 3 |
| 3 |
∴A1E=6-2
| 3 |
∵∠CA1B1=∠CAB=30°,
而∠AEA1=∠EA1D+∠EDA1=60°,
∴∠EDA1=30°,
∴ED=EA1=6-2
| 3 |
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰三角形的性质和含30度的直角三角形三边的关系.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
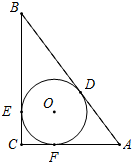 如图,在△ABC中,∠C=90°,⊙O是△ABC的内切圆,切点分别为D,E,F,若BD=6,AD=4,求⊙O的半径r.
如图,在△ABC中,∠C=90°,⊙O是△ABC的内切圆,切点分别为D,E,F,若BD=6,AD=4,求⊙O的半径r.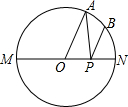 如图,MN是⊙O的直径,MN=2,点A在⊙O上,
如图,MN是⊙O的直径,MN=2,点A在⊙O上,
 如图A、B、C、D在同一直线上,BE⊥AD,CF⊥AD,垂足分别是B,C,AB=DC,AE=DF.求证:AF=DE.
如图A、B、C、D在同一直线上,BE⊥AD,CF⊥AD,垂足分别是B,C,AB=DC,AE=DF.求证:AF=DE.
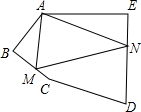 如图,在五边形ABCDE中,∠BAE=120°,∠B=∠E=90°,AB=BC,AE=DE,在边BC、DE上分别找一点M、N,使得△AMN周长最小,则∠AMN+∠ANM=
如图,在五边形ABCDE中,∠BAE=120°,∠B=∠E=90°,AB=BC,AE=DE,在边BC、DE上分别找一点M、N,使得△AMN周长最小,则∠AMN+∠ANM=