题目内容
问题情境:将一副直角三角板(Rt△ABC和Rt△DEF)按图(1)所示的方式摆放,其中∠ACB=90°,CA=CB,∠FDE=90°,∠E=30°,O是AB的中点,点D与点O重合,DF⊥AC于点M,DE⊥BC于点N.
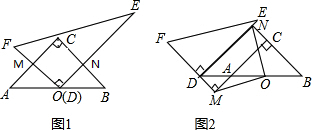
(1)试判断线段OM与ON的数量关系,并说明理由;
(2)将图(1)中的Rt△DEF沿着射线BA的方向平移至如图(2)的位置,使点D落在BA的延长线上,FD的延长线与CA的延长线垂直相交于点M,BC的延长线与DE垂直相交于点N,连结OM、ON.试判断线段OM、ON的数量关系与位置关系,并写出证明过程.

(1)试判断线段OM与ON的数量关系,并说明理由;
(2)将图(1)中的Rt△DEF沿着射线BA的方向平移至如图(2)的位置,使点D落在BA的延长线上,FD的延长线与CA的延长线垂直相交于点M,BC的延长线与DE垂直相交于点N,连结OM、ON.试判断线段OM、ON的数量关系与位置关系,并写出证明过程.
考点:全等三角形的判定与性质
专题:
分析:(1)根据等腰三角形的性质,可得两底角相等,根据线段中点的性质,可得OA=OB,根据AAS,可得两个三角形全等,根据全等三角形的性质,可得结果;
(2)根据四个角是直角的四边形是矩形,可得四边形DMCN是矩形,根据矩形的性质,可得对边相等,根据等腰三角形的判定,可得DM与AM的关系,根据根据SAS,可得三角形全等,根据全等三角形的性质,可得对应边相等,对应角相等,根据同角的余角相等,可得答案.
(2)根据四个角是直角的四边形是矩形,可得四边形DMCN是矩形,根据矩形的性质,可得对边相等,根据等腰三角形的判定,可得DM与AM的关系,根据根据SAS,可得三角形全等,根据全等三角形的性质,可得对应边相等,对应角相等,根据同角的余角相等,可得答案.
解答:证明:(1)∵CA=CB,
∴∠A=∠B,
∵O是AB的中点,
∴OA=OB.
∵DF⊥AC,DE⊥BC,
∴∠AMO=∠BNO=90°,
在△OMA和△ONB中,
,
∴△OMA≌△ONB(AAS),
∴OM=ON.
(2)解:OM=ON,OM⊥ON.
理由如下:连结OC,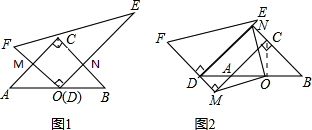
∵BN⊥DE,FM⊥CM,CM⊥BN,
∴四边形DMCN是矩形,
∴CN=DM,
∵∠DAM=∠CAB=45°,∠DMA=90°,
∴DM=MA,
∴CN=MA
∵∠ACB=90°,O为AB中点,
∴CO=
AB=AO,∠BCO=45°,CO⊥AB,
∴∠NCO=∠MAO=135°,
在△NOC和△MOA,
中
,
∴△NOC≌△MOA(SAS),
∴OM=ON,∠AOM=∠NOC,
∵∠NOC+∠AON=90°,
∴∠AOM+∠AON=90°,
∴∠MON=90°,
即OM⊥ON.
∴∠A=∠B,
∵O是AB的中点,
∴OA=OB.
∵DF⊥AC,DE⊥BC,
∴∠AMO=∠BNO=90°,
在△OMA和△ONB中,
|
∴△OMA≌△ONB(AAS),
∴OM=ON.
(2)解:OM=ON,OM⊥ON.
理由如下:连结OC,

∵BN⊥DE,FM⊥CM,CM⊥BN,
∴四边形DMCN是矩形,
∴CN=DM,
∵∠DAM=∠CAB=45°,∠DMA=90°,
∴DM=MA,
∴CN=MA
∵∠ACB=90°,O为AB中点,
∴CO=
| 1 |
| 2 |
∴∠NCO=∠MAO=135°,
在△NOC和△MOA,
中
|
∴△NOC≌△MOA(SAS),
∴OM=ON,∠AOM=∠NOC,
∵∠NOC+∠AON=90°,
∴∠AOM+∠AON=90°,
∴∠MON=90°,
即OM⊥ON.
点评:本题考查了全等三角形的判定与性质,(1)由SAS证明三角形全等,再由全等三角形的性质,得出答案;(2)先证明矩形,再由SAS证明三角形全等,证明全等三角形的对应边相等、对应角相等,同角的余角相等.

练习册系列答案
相关题目
若单项式4x2+ay2与
x2a-2y2是同类项,则a为( )
| 1 |
| 3 |
| A、-2 | B、2 | C、3 | D、4 |
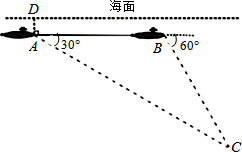 如图,一艘核潜艇在海面下500米A处测得俯角为30°正前方的海底C处有黑匣子信号发出,继续在同一深度直线航行4000米后在B处测得俯角为60°正前方的海底C处有黑匣子信号发出.点C和直线AB在同一铅垂面上,求点C距离海面的深度(结果保留根号).
如图,一艘核潜艇在海面下500米A处测得俯角为30°正前方的海底C处有黑匣子信号发出,继续在同一深度直线航行4000米后在B处测得俯角为60°正前方的海底C处有黑匣子信号发出.点C和直线AB在同一铅垂面上,求点C距离海面的深度(结果保留根号). 如图所示的图案是一个轴对称图形,若将其中的任意一个白色方块涂黑,所得的图案仍为轴对称图形的概率为
如图所示的图案是一个轴对称图形,若将其中的任意一个白色方块涂黑,所得的图案仍为轴对称图形的概率为