题目内容
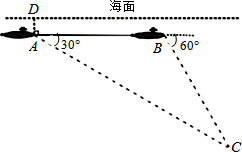 如图,一艘核潜艇在海面下500米A处测得俯角为30°正前方的海底C处有黑匣子信号发出,继续在同一深度直线航行4000米后在B处测得俯角为60°正前方的海底C处有黑匣子信号发出.点C和直线AB在同一铅垂面上,求点C距离海面的深度(结果保留根号).
如图,一艘核潜艇在海面下500米A处测得俯角为30°正前方的海底C处有黑匣子信号发出,继续在同一深度直线航行4000米后在B处测得俯角为60°正前方的海底C处有黑匣子信号发出.点C和直线AB在同一铅垂面上,求点C距离海面的深度(结果保留根号).考点:解直角三角形的应用-仰角俯角问题
专题:
分析:由C点向AB作垂线,交AB的延长线于E点,并交海面于F点,易证∠BAC=∠BCA,所以有BA=BC.然后在直角△BCE中,利用正弦函数求出CE.
解答: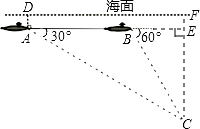 解:由C点向AB作垂线,交AB的延长线于E点,并交海面于F点.
解:由C点向AB作垂线,交AB的延长线于E点,并交海面于F点.
已知AB=4000(米),∠BAC=30°,∠EBC=60°,
∵∠BCA=∠EBC-∠BAC=30°,
∴∠BAC=∠BCA.
∴BC=BA=4000(米).
在Rt△BEC中,
EC=BC•sin60°=4000×
=2000
(米).
∴CF=CE+EF=2000
+500(米).
答:海底黑匣子C点处距离海面的深度为(2000
+500)米.
 解:由C点向AB作垂线,交AB的延长线于E点,并交海面于F点.
解:由C点向AB作垂线,交AB的延长线于E点,并交海面于F点.已知AB=4000(米),∠BAC=30°,∠EBC=60°,
∵∠BCA=∠EBC-∠BAC=30°,
∴∠BAC=∠BCA.
∴BC=BA=4000(米).
在Rt△BEC中,
EC=BC•sin60°=4000×
| ||
| 2 |
| 3 |
∴CF=CE+EF=2000
| 3 |
答:海底黑匣子C点处距离海面的深度为(2000
| 3 |
点评:本题考查了仰俯角问题,解决此类问题的关键是正确的将仰俯角转化为直角三角形的内角并选择正确的边角关系解直角三角形,要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目

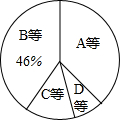 某校为了了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A、B、C、D四个等级,并绘制成下面的频数分布表(表一)和扇形统计图.
某校为了了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A、B、C、D四个等级,并绘制成下面的频数分布表(表一)和扇形统计图. 如图,在四边形ABCD中,给出下列三个论断:
如图,在四边形ABCD中,给出下列三个论断: