题目内容
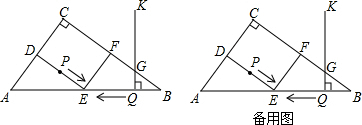
如图所示,在△ABC中,BC=40,AB=50,AC=30,D、E、F分别是AC、AB、BC的中点,点P从点D出发沿折线DE-EF-FC-CD以7个单位长度/秒的速度匀速运动;点Q从点B出发沿BA方向以4个单位长度/秒的速度匀速运动,过Q点作射线QKWAB,交折线BC-CA于点G.点P、Q运动的时间是t秒(t>0).
(1)△ABC的形状是 (直接填写结论);
(2)当点P运动到折线EF-FC上,且点P又恰好落在射线QK上时,求t的值;
(3)射线QK能否把四边形CDEF分成周长相等的两部分?若能,求出t的值;若不能,说明理由.
(1)△ABC的形状是
(2)当点P运动到折线EF-FC上,且点P又恰好落在射线QK上时,求t的值;
(3)射线QK能否把四边形CDEF分成周长相等的两部分?若能,求出t的值;若不能,说明理由.

考点:相似形综合题
专题:
分析:(1)由勾股定理可以判定)△ABC的形状是直角三角形.
(2))①当点P在EF上(2
≤t≤5)时根据△PQE∽△BCA,根据相似三角形的对应边的比相等,可以求出t的值;
②当点P在FC上(5≤t≤7
)时,PB=PF+BF就可以得到;
(3)连接DF,过点F作FH⊥AB于点H,由四边形CDEF为矩形,QK把矩形CDEF分为周长相等的两部分,根据△HBF∽△CBA,对应边的比相等,就可以求得t的值;
(2))①当点P在EF上(2
| 6 |
| 7 |
②当点P在FC上(5≤t≤7
| 6 |
| 7 |
(3)连接DF,过点F作FH⊥AB于点H,由四边形CDEF为矩形,QK把矩形CDEF分为周长相等的两部分,根据△HBF∽△CBA,对应边的比相等,就可以求得t的值;
解答:解:(1)∵在△ABC中,BC=40,AB=50,AC=30,
∴AB2=BC2+AC2,
∴△ABC的形状是直角三角形.
(2)①当点P在EF上(2
≤t≤5)时,
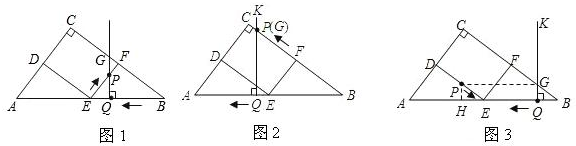
如图1,QB=4t,DE+EP=7t
由△PQE∽△BCA,得
=
∴t=4
.
②当点P在FC上(5≤t≤7
)时,
如图2,已知QB=4t,从而cosB=
=
=
∴PB=5t,
由PF=7t-35,BF=20,得5t=7t-35+20.
解得t=
.
(3)射线QK能把四边形CDEF分成周长相等的两部分.
如图3,连接DF,过点P作PH⊥AB于点H,
∵D,F是AC,BC的中点,
∴DE∥BC,EF∥AC,四边形CDEF为矩形
∴QK过DF的中点O时,QK把矩形CDEF分为周长相等的两部分,
此时QH=OF=12.5.由BF=20,△HBF∽△CBA,得HB=16.
故t=
=
=
.
∴AB2=BC2+AC2,
∴△ABC的形状是直角三角形.
(2)①当点P在EF上(2
| 6 |
| 7 |
如图1,QB=4t,DE+EP=7t
由△PQE∽△BCA,得
| 7t-20 |
| 50 |
| 25-4t |
| 30 |
∴t=4
| 21 |
| 41 |
②当点P在FC上(5≤t≤7
| 6 |
| 7 |
如图2,已知QB=4t,从而cosB=
| QB |
| PB |
| 4t |
| PB |
| 4 |
| 5 |
∴PB=5t,
由PF=7t-35,BF=20,得5t=7t-35+20.
解得t=
| 15 |
| 2 |
(3)射线QK能把四边形CDEF分成周长相等的两部分.
如图3,连接DF,过点P作PH⊥AB于点H,
∵D,F是AC,BC的中点,
∴DE∥BC,EF∥AC,四边形CDEF为矩形
∴QK过DF的中点O时,QK把矩形CDEF分为周长相等的两部分,
此时QH=OF=12.5.由BF=20,△HBF∽△CBA,得HB=16.
故t=
| QH+HB |
| 4 |
| 12.5+16 |
| 4 |
| 57 |
| 8 |

点评:本题主要运用了相似三角形性质,对应边的比相等,正确找出题目中的相似三角形是解题的关键.在本题中还要学会分类讨论的思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.
如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.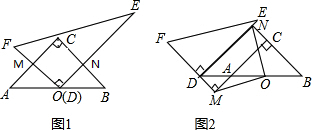

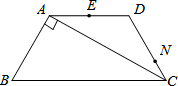 如图,已知等腰梯形ABCD,AD∥BC,AB⊥AC,AB=AD=DC=4cm,点N在DC上,且CN=1cm,E是AD的中点,请在对角线AC上找一点M,使EM+MN的值最小,最小值为
如图,已知等腰梯形ABCD,AD∥BC,AB⊥AC,AB=AD=DC=4cm,点N在DC上,且CN=1cm,E是AD的中点,请在对角线AC上找一点M,使EM+MN的值最小,最小值为