题目内容
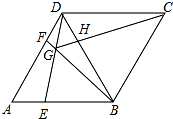 如图,在菱形ABCD中,AB=BD,点E,F分别在AB,AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H,下列结论:①△AED≌△DFB;②S四边形BCDG=CG2;③若AF=2DF,则BG=6GF.其中正确的结论是( )
如图,在菱形ABCD中,AB=BD,点E,F分别在AB,AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H,下列结论:①△AED≌△DFB;②S四边形BCDG=CG2;③若AF=2DF,则BG=6GF.其中正确的结论是( )| A、只有①② | B、①②③ |
| C、只有②③ | D、只有①③ |
考点:菱形的性质,全等三角形的判定与性质
专题:
分析:①先证明△ABD为等边三角形,根据“SAS”证明△AED≌△DFB;
②证明∠BGE=60°=∠BCD,从而得点B、C、D、G四点共圆,因此∠BGC=∠DGC=60°,过点C作CM⊥GB于M,CN⊥GD于N.证明△CBM≌△CDN,所以S四边形BCDG=S四边形CMGN,易求后者的面积.
③过点F作FP∥AE于P点,根据题意有FP:AE=DF:DA=1:3,则FP:BE=1:6=FG:BG,即BG=6GF.
②证明∠BGE=60°=∠BCD,从而得点B、C、D、G四点共圆,因此∠BGC=∠DGC=60°,过点C作CM⊥GB于M,CN⊥GD于N.证明△CBM≌△CDN,所以S四边形BCDG=S四边形CMGN,易求后者的面积.
③过点F作FP∥AE于P点,根据题意有FP:AE=DF:DA=1:3,则FP:BE=1:6=FG:BG,即BG=6GF.
解答:解:①∵四边形ABCD为菱形,
∴AB=AD.
∵AB=BD,
∴△ABD为等边三角形.
∴∠A=∠BDF=60°.
又∵AE=DF,AD=BD,
∴△AED≌△DFB,故本小题正确;

②∵∠BGE=∠BDG+∠DBF=∠BDG+∠GDF=60°=∠BCD,
即∠BGD+∠BCD=180°,
∴点B、C、D、G四点共圆,
∴∠BGC=∠BDC=60°,∠DGC=∠DBC=60°.
∴∠BGC=∠DGC=60°.
过点C作CM⊥GB于M,CN⊥GD于N.
则△CBM≌△CDN,(AAS)
∴S四边形BCDG=S四边形CMGN.
S四边形CMGN=2S△CMG,
∵∠CGM=60°,
∴GM=
CG,CM=
CG,
∴S四边形CMGN=2S△CMG=2×
×
CG×
CG=
CG2,故本小题错误;
③过点F作FP∥AE于P点.
∵AF=2FD,
∴FP:AE=DF:DA=1:3,
∵AE=DF,AB=AD,
∴BE=2AE,
∴FP:BE=1:6=FG:BG,
即BG=6GF,故本小题正确.
综上所述,正确的结论有①③.
故选D.
∴AB=AD.
∵AB=BD,
∴△ABD为等边三角形.
∴∠A=∠BDF=60°.
又∵AE=DF,AD=BD,
∴△AED≌△DFB,故本小题正确;

②∵∠BGE=∠BDG+∠DBF=∠BDG+∠GDF=60°=∠BCD,
即∠BGD+∠BCD=180°,
∴点B、C、D、G四点共圆,
∴∠BGC=∠BDC=60°,∠DGC=∠DBC=60°.
∴∠BGC=∠DGC=60°.
过点C作CM⊥GB于M,CN⊥GD于N.
则△CBM≌△CDN,(AAS)
∴S四边形BCDG=S四边形CMGN.
S四边形CMGN=2S△CMG,
∵∠CGM=60°,
∴GM=
| 1 |
| 2 |
| ||
| 2 |
∴S四边形CMGN=2S△CMG=2×
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
③过点F作FP∥AE于P点.
∵AF=2FD,

∴FP:AE=DF:DA=1:3,
∵AE=DF,AB=AD,
∴BE=2AE,
∴FP:BE=1:6=FG:BG,
即BG=6GF,故本小题正确.
综上所述,正确的结论有①③.
故选D.
点评:此题综合考查了菱形的性质,等边三角形的判定与性质,全等三角形的判定和性质,作出辅助线构造出全等三角形,把不规则图形的面转化为两个全等三角形的面积是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
已知a<b,则下列不等式一定成立的是( )
| A、a+3>b+3 |
| B、2a>2b |
| C、-b>-a |
| D、b-a>0 |
 如图所示,在Rt△ABC中,∠C=90°,∠B=2∠A,AB=6cm,则BC的长是( )
如图所示,在Rt△ABC中,∠C=90°,∠B=2∠A,AB=6cm,则BC的长是( )| A、2cm | B、4cm |
| C、6cm | D、3cm |
△ABC中,AB=AC,AB边的中垂线与直线AC所成的角为50°,则∠B等于( )
| A、70° |
| B、20°或70° |
| C、40°或70° |
| D、40°或20° |
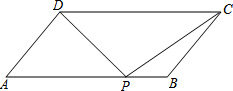 如图,平行四边形ABCD中,AB+BC=20,sinA=
如图,平行四边形ABCD中,AB+BC=20,sinA=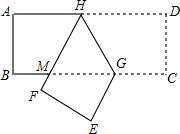 如图,已知在长方形纸条ABCD中,点G在边BC上,BG=2CG,将该纸条沿着过点G的直线翻折后,点C、D分别落在边BC下方的点E、F处,且点E、F、B在同一条直线上,折痕与边AD交于点H,HF与BG交于点M.设AB=t,那么△GHM的周长为
如图,已知在长方形纸条ABCD中,点G在边BC上,BG=2CG,将该纸条沿着过点G的直线翻折后,点C、D分别落在边BC下方的点E、F处,且点E、F、B在同一条直线上,折痕与边AD交于点H,HF与BG交于点M.设AB=t,那么△GHM的周长为 如图,已知AC平分∠DAB,E为AC上一点,AD=AB,那么△CDE≌△CBE,为什么?
如图,已知AC平分∠DAB,E为AC上一点,AD=AB,那么△CDE≌△CBE,为什么?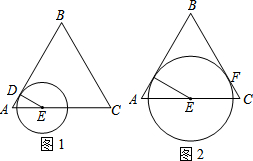 己知等边△ABC,边长为4,点D从点A出发,沿AB运动到点B,到点B停止运动.点E从A出发,沿AC的方向在直线AC上运动.点D的速度为每秒1个单位,点E的速度为每秒2个单位,它们同时出发,同时停止.以点E为圆心,DE长为半径作圆.设E点的运动时间为t秒,
己知等边△ABC,边长为4,点D从点A出发,沿AB运动到点B,到点B停止运动.点E从A出发,沿AC的方向在直线AC上运动.点D的速度为每秒1个单位,点E的速度为每秒2个单位,它们同时出发,同时停止.以点E为圆心,DE长为半径作圆.设E点的运动时间为t秒,