题目内容
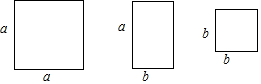
13. 如图,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,请按照图中所标注的数据计算图中实线所围成的图形的面积S=50.
如图,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,请按照图中所标注的数据计算图中实线所围成的图形的面积S=50.
分析 求出∠F=∠AGB=∠EAB=90°,∠FEA=∠BAG,根据AAS证△FEA≌△GAB,推出AG=EF=6,AF=BG=2,同理CG=DH=4,BG=CH=2,求出FH=14,根据阴影部分的面积=S梯形EFHD-S△EFA-S△ABC-S△DHC和面积公式代入求出即可.
解答 解:∵AE⊥AB,EF⊥AF,BG⊥AG,
∴∠F=∠AGB=∠EAB=90°,
∴∠FEA+∠EAF=90°,∠EAF+∠BAG=90°,
∴∠FEA=∠BAG,
在△FEA和△GAB中
∵$\left\{\begin{array}{l}{∠F=∠BGA}\\{∠FEA=∠BAG}\\{AE=AB}\end{array}\right.$,
∴△FEA≌△GAB(AAS),
∴AG=EF=6,AF=BG=2,
同理CG=DH=4,BG=CH=2,
∴FH=2+6+4+2=14,
∴梯形EFHD的面积是$\frac{1}{2}$×(EF+DH)×FH=$\frac{1}{2}$×(6+4)×14=70,
∴阴影部分的面积是S梯形EFHD-S△EFA-S△ABC-S△DHC
=70-$\frac{1}{2}$×6×2-$\frac{1}{2}$×(6+4)×2-$\frac{1}{2}$×4×2
=50.
故答案为50.
点评 本题考查了三角形的面积,梯形的面积,全等三角形的性质和判定等知识点,关键是把不规则图形的面积转化成规则图形的面积.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
8.已知方程x2+2x-1=0,则此方程( )
| A. | 无实数根 | B. | 两根之和为2 | C. | 两根之积为-1 | D. | 有一个根为$1+\sqrt{2}$ |
9.下列命题中,假命题是( )
| A. | 矩形的对角线相等 | |
| B. | 菱形的面积等于两条对角线乘积的一半 | |
| C. | 对角线互相垂直的矩形是正方形 | |
| D. | 有两个角相等的梯形是等腰梯形 |
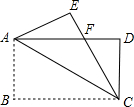 如图,将矩形ABCD沿对角线AC对折,使△ABC落在△ACE的位置,且CE与AD相交于点F,连结ED,若AB=$\sqrt{3}$,BC=3.
如图,将矩形ABCD沿对角线AC对折,使△ABC落在△ACE的位置,且CE与AD相交于点F,连结ED,若AB=$\sqrt{3}$,BC=3.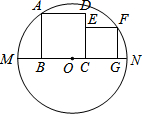 如图,两个正方形都在⊙O的直径MN的同侧,顶点B、C、G都在MN上,正方形ABCD的顶点A和正方形CEFG的顶点F都在⊙O上,点E在CD上.若AB=5,FG=3,则OC的长为2.
如图,两个正方形都在⊙O的直径MN的同侧,顶点B、C、G都在MN上,正方形ABCD的顶点A和正方形CEFG的顶点F都在⊙O上,点E在CD上.若AB=5,FG=3,则OC的长为2.