题目内容
2.顺次连接A、B.C,D得到平行四边形ABCD,已知AB=4,BC=6,∠B=60°.则此平行四边形面积是12$\sqrt{3}$.分析 作AE⊥BC于E,根据S平行四边形ABCD=BC•AE,先求出AE即可求解.
解答 解: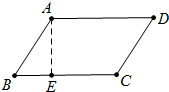 如图作AE⊥BC于E.
如图作AE⊥BC于E.
在RT△ABE中,∵∠AEB=90°,AB=4,∠B=60°,
∴BE=$\frac{1}{2}$AB=2,AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∵四边形ABCD是平行四边形,
∴S平行四边形ABCD=BC•AE=6×$2\sqrt{3}$=12$\sqrt{3}$.
故答案为12$\sqrt{3}$.
点评 本题考查平行四边形的性质、直角三角形30度角的性质等知识,解题的关键是记住平行四边形的面积公式,平行四边形的面积等于底乘高,所以中考常考题型.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
10. 如图,在边长为12的正方形ABCD中,有一个小正方形EFGH,其中E、F分别在AB、BC上,FG在Rt△DCF上,若BF=3,则BE的长为( )
如图,在边长为12的正方形ABCD中,有一个小正方形EFGH,其中E、F分别在AB、BC上,FG在Rt△DCF上,若BF=3,则BE的长为( )
 如图,在边长为12的正方形ABCD中,有一个小正方形EFGH,其中E、F分别在AB、BC上,FG在Rt△DCF上,若BF=3,则BE的长为( )
如图,在边长为12的正方形ABCD中,有一个小正方形EFGH,其中E、F分别在AB、BC上,FG在Rt△DCF上,若BF=3,则BE的长为( )| A. | 1 | B. | $\frac{5}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{9}{4}$ |
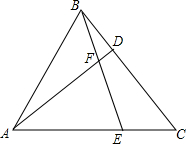 如图,在等边△ABC中,点D、E分别在BC、AC边上,BD=CE,AD与BE相交于点F.
如图,在等边△ABC中,点D、E分别在BC、AC边上,BD=CE,AD与BE相交于点F.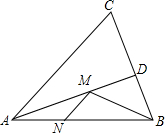 如图,在锐角△ABC中,AB=6,∠BAC=60°,∠BAC的平分线交BC于点D,M、N是AD、AB上的动点,则BM+MN的最小值为3$\sqrt{3}$.
如图,在锐角△ABC中,AB=6,∠BAC=60°,∠BAC的平分线交BC于点D,M、N是AD、AB上的动点,则BM+MN的最小值为3$\sqrt{3}$.