题目内容
11.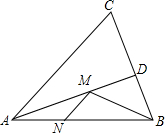 如图,在锐角△ABC中,AB=6,∠BAC=60°,∠BAC的平分线交BC于点D,M、N是AD、AB上的动点,则BM+MN的最小值为3$\sqrt{3}$.
如图,在锐角△ABC中,AB=6,∠BAC=60°,∠BAC的平分线交BC于点D,M、N是AD、AB上的动点,则BM+MN的最小值为3$\sqrt{3}$.
分析 在AC上取一点E,使得AE=AB,过E作EN⊥AB于N,交AD于M,连接BM,BE,BE交AD于O,根据两点之间线段最短和垂线段最短得出此时BM+MN最小,求出E和B关于AD对称,求出BM+MN′=EN′,求出EN′,即可求出答案.
解答 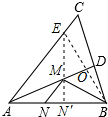 解:在AC上取一点E,使得AE=AB,过E作EN⊥AB于N′,交AD于M,连接BM,BE,BE交AD于O,则BM+MN最小(根据两点之间线段最短;点到直线垂直距离最短),
解:在AC上取一点E,使得AE=AB,过E作EN⊥AB于N′,交AD于M,连接BM,BE,BE交AD于O,则BM+MN最小(根据两点之间线段最短;点到直线垂直距离最短),
∵AD平分∠CAB,AE=AB,
∴EO=OB,AD⊥BE,
∴AD是BE的垂直平分线(三线合一),
∴E和B关于直线AD对称,
∴EM=BM,
即BM+MN′=EM+MN′=EN′,
∵EN′⊥AB,
∴∠ENA=90°,
∵∠CAB=60°,
∴∠AEN′=30°,
∵AE=AB=6,
∴AN=$\frac{1}{2}$AE=3,
在△AEN中,由勾股定理得:EN=$\sqrt{A{E}^{2}-AN{′}^{2}}$=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$,即BM+MN的最小值是3$\sqrt{3}$.
故答案为:3$\sqrt{3}$.
点评 本题考查的是轴对称-最短路线问题,涉及到垂线的性质,勾股定理,含30度角的直角三角形性质,轴对称的性质,等腰三角形的性质等知识点的综合运用.

练习册系列答案
相关题目
16.计算$\frac{m}{2m+1}+\frac{m+1}{2m+1}$的值是( )
| A. | 0 | B. | 2 | C. | -1 | D. | 1 |
 如图,四边形ABCD是边长为2的正方形,△CDE是等边三角形.
如图,四边形ABCD是边长为2的正方形,△CDE是等边三角形.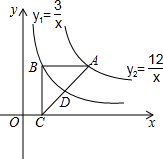 如图是反比例函数${y_1}=\frac{3}{x}$和${y_2}=\frac{12}{x}$在第一象限的图象,等腰直角△ABC的直角顶点B在y1上,顶点A在y2上,顶点C在x轴上,AB∥x轴,则CD:AD=$\frac{\sqrt{13}+1}{6}$.
如图是反比例函数${y_1}=\frac{3}{x}$和${y_2}=\frac{12}{x}$在第一象限的图象,等腰直角△ABC的直角顶点B在y1上,顶点A在y2上,顶点C在x轴上,AB∥x轴,则CD:AD=$\frac{\sqrt{13}+1}{6}$.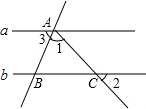 如图所示,已知a∥b,∠1=72°,∠2=40°,则∠3=68°.
如图所示,已知a∥b,∠1=72°,∠2=40°,则∠3=68°.