题目内容
17.在反比例函数y=$\frac{2-5m}{x}$图象上有两点P(x1,y1),Q(x2,y2),若x1>0>x2,y1>y2,则m的取值范围是m<$\frac{2}{5}$.分析 由于x1>0>x2,y1>y2,则反比例函数图象分布在第一、三象限,则2-5m>0,然后解不等式即可.
解答 解:∵x1>0>x2,y1>y2,
∴2-5m>0,
∴m<$\frac{2}{5}$.
故答案为m<$\frac{2}{5}$.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.也考查了反比例函数的性质.

练习册系列答案
相关题目
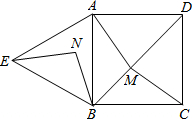 如图,△ABE是等边三角形,M是正方形ABCD对角线BD(不含B点)上任意一点,BM=BN,∠ABN=15°(点N在AB的左侧),当AM+BM+CM的最小值为$\sqrt{3}$+1时,正方形的边长为$\sqrt{2}$.
如图,△ABE是等边三角形,M是正方形ABCD对角线BD(不含B点)上任意一点,BM=BN,∠ABN=15°(点N在AB的左侧),当AM+BM+CM的最小值为$\sqrt{3}$+1时,正方形的边长为$\sqrt{2}$.