题目内容
12.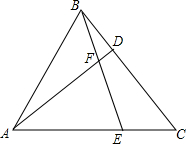 如图,在等边△ABC中,点D、E分别在BC、AC边上,BD=CE,AD与BE相交于点F.
如图,在等边△ABC中,点D、E分别在BC、AC边上,BD=CE,AD与BE相交于点F.(1)求证:△BDF∽△ADB;
(2)当$\frac{BD}{CD}$=$\frac{1}{2}$时,求$\frac{DF}{AF}$的值.
分析 (1)利用等边三角形的性质可证明△ABD≌△BCE,可得∠FBD=∠BAD,可证明△BDF∽△ADB;
(2)根据$\frac{BD}{CD}$=$\frac{1}{2}$,得到$\frac{CE}{AE}$=$\frac{1}{2}$,过E作EG∥AD交CD于G,根据相似三角形的性质得到$\frac{GE}{AD}=\frac{CE}{AC}$=$\frac{CG}{CD}$=$\frac{1}{3}$,求得AD=3GE,DG=$\frac{2}{3}$CD,通过△BDF∽△BEG,得到$\frac{DF}{EG}=\frac{BD}{BG}$=$\frac{3}{7}$,得到DF=$\frac{3}{7}$EG,于是得到结论.
解答 (1)证明:∵△ABC为等边三角形,
∴AB=BC,∠ABC=∠C,
在△ABD和△BCE中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABD=∠C}\\{BD=CE}\end{array}\right.$,
∴△ABD≌△BCE(SAS),
∴∠FBD=∠BAD,且∠BDF=∠ADB,
∴△BDF∽△ADB;
(2)∵BD=CE,AC=BC,
∴CD=AE,
∵$\frac{BD}{CD}$=$\frac{1}{2}$,
∴$\frac{CE}{AE}$=$\frac{1}{2}$,
过E作EG∥AD交CD于G,
∴△CEG∽△ACD,
∴$\frac{GE}{AD}=\frac{CE}{AC}$=$\frac{CG}{CD}$=$\frac{1}{3}$,
∴$\frac{DG}{CD}$=$\frac{2}{3}$,AD=3GE,
∴DG=$\frac{2}{3}$CD,
∵BD=$\frac{1}{2}$CD,
∴$\frac{BD}{DG}$=$\frac{3}{4}$,
∵EG∥AD,
∴△BDF∽△BEG,
∴$\frac{DF}{EG}=\frac{BD}{BG}$=$\frac{3}{7}$,
∴DF=$\frac{3}{7}$EG,
∴AF=AD-DF=$\frac{19}{7}$EG,
∴$\frac{DF}{AF}$=$\frac{3}{19}$.
点评 本题主要考查了相似三角形的判定和性质,全等三角形的判定和性质,等边三角形的性质,准确作出辅助线是解题的关键.

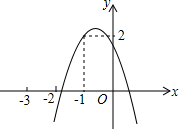 如图,二次函数y=ax2+bx+c的图象经过点(-1,2),且与x轴交点的横坐标分别为x1、x2,-2<x1<-1,0<x2<1,下列结论:
如图,二次函数y=ax2+bx+c的图象经过点(-1,2),且与x轴交点的横坐标分别为x1、x2,-2<x1<-1,0<x2<1,下列结论:①4a-2b+c<0;
②2a-b<0;
③b2+8a>4ac;
④b<-1.
其中正确的有 ( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 甲班 | 8 | 7 | 7 | 4 | 8 | 7 | 8 | 8 | 8 | 8 |
| 乙班 | 7 | 8 | 8 | 10 | 7 | 7 | 8 | 7 | 7 | 7 |
(2)采用怎样的方法,对参赛班级更为公平?若采用你提供的方法,甲、乙两班哪个班获胜?
| A. | 1 | B. | -2 | C. | 0 | D. | -0.5 |
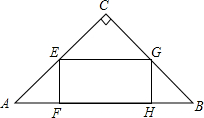 如图,矩形EFGH的顶点F,G在等腰Rt△ABC的斜边AB上,点E,H分别在直角边AC和BC上,EF=$\frac{1}{2}$EH,AB=6cm,求矩形EFGH的周长.
如图,矩形EFGH的顶点F,G在等腰Rt△ABC的斜边AB上,点E,H分别在直角边AC和BC上,EF=$\frac{1}{2}$EH,AB=6cm,求矩形EFGH的周长. 如图,四边形ABCD是边长为2的正方形,△CDE是等边三角形.
如图,四边形ABCD是边长为2的正方形,△CDE是等边三角形.