题目内容
10. 如图,在边长为12的正方形ABCD中,有一个小正方形EFGH,其中E、F分别在AB、BC上,FG在Rt△DCF上,若BF=3,则BE的长为( )
如图,在边长为12的正方形ABCD中,有一个小正方形EFGH,其中E、F分别在AB、BC上,FG在Rt△DCF上,若BF=3,则BE的长为( )| A. | 1 | B. | $\frac{5}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{9}{4}$ |
分析 由在边长为12的正方形ABCD中,有一个小正方形EFGH,根据同角的余角相等,可得∠BEF=∠CDF,继而证得△BEF∽△CFD,然后由相似三角形的对应边成比例,求得BE长.
解答 解:∵四边形ABCD是正方形,
∴∠B=∠C=90°,
在△BEF与△CFD中
∵∠BFE+∠CFD=∠CFD+∠CDF=90°,
∴∠BEF=∠CDF,
∴△BEF∽△CFD,
∴$\frac{BF}{CD}=\frac{BE}{CF}$,
∵BF=3,BC=12,
∴CF=BC-BF=12-3=9,
∴$\frac{3}{12}=\frac{BE}{9}$,
解得:BE=$\frac{9}{4}$.
故选D.
点评 此题考查了相似三角形的判定与性质、正方形的性质以及直角三角形的性质.熟练掌握正方形的性质,证明三角形相似得出比例式是解决问题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
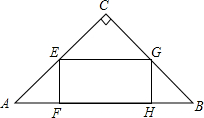 如图,矩形EFGH的顶点F,G在等腰Rt△ABC的斜边AB上,点E,H分别在直角边AC和BC上,EF=$\frac{1}{2}$EH,AB=6cm,求矩形EFGH的周长.
如图,矩形EFGH的顶点F,G在等腰Rt△ABC的斜边AB上,点E,H分别在直角边AC和BC上,EF=$\frac{1}{2}$EH,AB=6cm,求矩形EFGH的周长. 如图,四边形ABCD是边长为2的正方形,△CDE是等边三角形.
如图,四边形ABCD是边长为2的正方形,△CDE是等边三角形.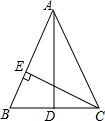 如图,在△ABC中,AB=AC=13,BC=10,D是BC的中点,CE⊥AB于E.
如图,在△ABC中,AB=AC=13,BC=10,D是BC的中点,CE⊥AB于E.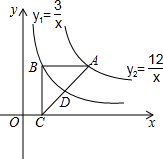 如图是反比例函数${y_1}=\frac{3}{x}$和${y_2}=\frac{12}{x}$在第一象限的图象,等腰直角△ABC的直角顶点B在y1上,顶点A在y2上,顶点C在x轴上,AB∥x轴,则CD:AD=$\frac{\sqrt{13}+1}{6}$.
如图是反比例函数${y_1}=\frac{3}{x}$和${y_2}=\frac{12}{x}$在第一象限的图象,等腰直角△ABC的直角顶点B在y1上,顶点A在y2上,顶点C在x轴上,AB∥x轴,则CD:AD=$\frac{\sqrt{13}+1}{6}$.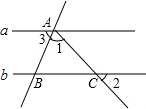 如图所示,已知a∥b,∠1=72°,∠2=40°,则∠3=68°.
如图所示,已知a∥b,∠1=72°,∠2=40°,则∠3=68°.