题目内容
16．
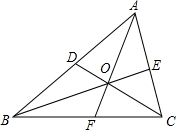如图，在△ABC中，∠BAC、∠ABC的平分线AF、BE交于点O，连接CD并延长交AB边于点D，则CD是△ABC的（ ）| A． | 角平分线 | B． | 中线 | C． | 高 | D． | 以上都不对 |
分析 根据三角形的三个内角的平分线交于一点，根据题意，可知CD是△ABC的角平分线．
解答 解：∵∠A、∠B的平分线交于点O，三角形的三个内角的平分线交于一点，
∴∠ACB的平分线也过0点，
∴CD是△ABC的角平分线．
故选A．
点评 本题主要考查了三角形的角平分线，掌握三角形的三条角平分线相交于一点，是解答本题的关键，一个内角的平分线与这个内角的对边交于一点，则这个内角的顶点与所交的点间的线段叫做三角形的角平分线．
练习册系列答案
导学教程高中新课标系列答案
相关题目
4．对于一元二次方程ax2+bx+c=0（a≠0），有下列说法：
①当a＜0，且b＞a+c时，方程一定有实数根；
②若ac＜0，则方程有两个不相等的实数根；
③若a-b+c=0，则方程一定有一个根为-1；
④若方程有两个不相等的实数根，则方程bx2+ax+c=0一定有两个不相等的实数根．
其中正确的有（ ）
①当a＜0，且b＞a+c时，方程一定有实数根；
②若ac＜0，则方程有两个不相等的实数根；
③若a-b+c=0，则方程一定有一个根为-1；
④若方程有两个不相等的实数根，则方程bx2+ax+c=0一定有两个不相等的实数根．
其中正确的有（ ）
| A． | ①②③ | B． | ①②④ | C． | ②③ | D． | ①②③④ |
8．方程x2+16=8x的根的情况为（ ）
| A． | 有两个不相等的实数根 | B． | 有两个相等的实数根 | ||
| C． | 有一个实数根 | D． | 没有实数根 |
如图所示，在△ABC中，AD是它的角平分线，AB=7cm，AC=4cm，则S△ABD：S△ACD=7：4．