题目内容
5．
如图所示，在△ABC中，AD是它的角平分线，AB=7cm，AC=4cm，则S△ABD：S△ACD=7：4．
分析 根据角平分线的性质，可得出△ABD的边AB上的高与△ACD的AC上的高相等，根据三角形的面积公式，即可得出△ABD与△ACD的面积之比等于对应边之比．
解答 解：∵AD是△ABC的角平分线，
∴设△ABD的边AB上的高与△ACD的AC上的高分别为h1，h2，
∴h1=h2，
∴S△ABD：S△ACD═AB：AC=7：4，
故答案为7：4．
点评 本题考查了角平分线的性质，以及三角形的面积公式，熟练掌握三角形角平分线的性质是解题的关键．
练习册系列答案
快乐5加2金卷系列答案
相关题目
15．
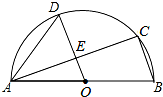如图，AB是半圆O的直径，C、D是半圆O上的两点，OD∥BC，OD与AC交于点E．下列结论不一定成立的是（ ）
如图，AB是半圆O的直径，C、D是半圆O上的两点，OD∥BC，OD与AC交于点E．下列结论不一定成立的是（ ）| A． | △AOD是等边三角形 | B． | $\widehat{AD}$=$\widehat{CD}$ | ||
| C． | ∠ACB=90° | D． | OE=$\frac{1}{2}$BC |
16．
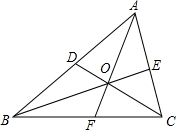如图，在△ABC中，∠BAC、∠ABC的平分线AF、BE交于点O，连接CD并延长交AB边于点D，则CD是△ABC的（ ）
如图，在△ABC中，∠BAC、∠ABC的平分线AF、BE交于点O，连接CD并延长交AB边于点D，则CD是△ABC的（ ）| A． | 角平分线 | B． | 中线 | C． | 高 | D． | 以上都不对 |
如图，BD是△ABC的中线，AB=6cm，BC=4cm，则△ABD和△BCD的周长差为2cm．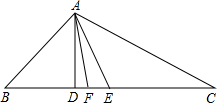
如图，完成下面几何语言的表达．
如图，在四边形ABCD中，∠BAD=90°，∠CBD=90°，且AD=4，AB=3，BC=12．求正方形DCEF的面积．
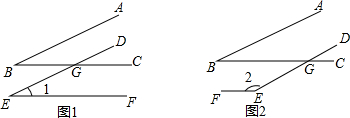
一个正方体的平面展开图如图所示，将它折成正方体后“建”字对面是作．