题目内容
4.对于一元二次方程ax2+bx+c=0(a≠0),有下列说法:①当a<0,且b>a+c时,方程一定有实数根;
②若ac<0,则方程有两个不相等的实数根;
③若a-b+c=0,则方程一定有一个根为-1;
④若方程有两个不相等的实数根,则方程bx2+ax+c=0一定有两个不相等的实数根.
其中正确的有( )
| A. | ①②③ | B. | ①②④ | C. | ②③ | D. | ①②③④ |
分析 利用根的判别式△=b2-4ac,结合字母的取值,逐一探讨得出答案即可.
解答 解:①由a<0,且b>a+c,得出(a+c)2<b2,△=b2-4ac=(a+c)2-4ac=(a-c)2≥0,关于x的方程ax2+bx+c=0必有实根;故①正确;
②若ac<0,a、c异号,则△=b2-4ac>0,方程ax2+bx+c=0一定有实数根,所以②正确;
③若a-b+c=0,b=a+c,△=b2-4ac=(a+c)2-4ac=(a-c)2≥0,则一元二次方程ax2+bx+c=0有两个实数根,所以③错误;
④若方程ax2+bx+c=0有两个不相等的实数根,c可能为0,则方程bx2+ax+c=0,a2-4bc>0一定有两个不相等的实数根,所以④正确.
故选:B.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
相关题目
14.张大伯由于年龄的缘故,忘了11位手机号码中最后两位号码,那么张大伯最多需要拨号( )次,才能拨对号码?
| A. | 1次 | B. | 50次 | C. | 100次 | D. | 200次 |
15.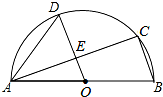 如图,AB是半圆O的直径,C、D是半圆O上的两点,OD∥BC,OD与AC交于点E.下列结论不一定成立的是( )
如图,AB是半圆O的直径,C、D是半圆O上的两点,OD∥BC,OD与AC交于点E.下列结论不一定成立的是( )
 如图,AB是半圆O的直径,C、D是半圆O上的两点,OD∥BC,OD与AC交于点E.下列结论不一定成立的是( )
如图,AB是半圆O的直径,C、D是半圆O上的两点,OD∥BC,OD与AC交于点E.下列结论不一定成立的是( )| A. | △AOD是等边三角形 | B. | $\widehat{AD}$=$\widehat{CD}$ | ||
| C. | ∠ACB=90° | D. | OE=$\frac{1}{2}$BC |
19.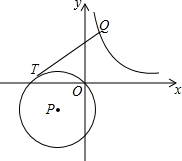 如图,在平面直角坐标系中,⊙P的圆心坐标是(-1,-1),半径为$\sqrt{2}$,点Q是函数y=$\frac{1}{x}$的图象上一动点,过点Q作⊙P的切线QT,切点为T,则线段QT长度的最小值为( )
如图,在平面直角坐标系中,⊙P的圆心坐标是(-1,-1),半径为$\sqrt{2}$,点Q是函数y=$\frac{1}{x}$的图象上一动点,过点Q作⊙P的切线QT,切点为T,则线段QT长度的最小值为( )
 如图,在平面直角坐标系中,⊙P的圆心坐标是(-1,-1),半径为$\sqrt{2}$,点Q是函数y=$\frac{1}{x}$的图象上一动点,过点Q作⊙P的切线QT,切点为T,则线段QT长度的最小值为( )
如图,在平面直角坐标系中,⊙P的圆心坐标是(-1,-1),半径为$\sqrt{2}$,点Q是函数y=$\frac{1}{x}$的图象上一动点,过点Q作⊙P的切线QT,切点为T,则线段QT长度的最小值为( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{6}$ | D. | 4 |
16.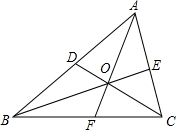 如图,在△ABC中,∠BAC、∠ABC的平分线AF、BE交于点O,连接CD并延长交AB边于点D,则CD是△ABC的( )
如图,在△ABC中,∠BAC、∠ABC的平分线AF、BE交于点O,连接CD并延长交AB边于点D,则CD是△ABC的( )
 如图,在△ABC中,∠BAC、∠ABC的平分线AF、BE交于点O,连接CD并延长交AB边于点D,则CD是△ABC的( )
如图,在△ABC中,∠BAC、∠ABC的平分线AF、BE交于点O,连接CD并延长交AB边于点D,则CD是△ABC的( )| A. | 角平分线 | B. | 中线 | C. | 高 | D. | 以上都不对 |
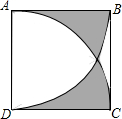 如图,正方形ABCD的边长为1,分别以A、D为圆心,1为半径画弧BD、AC,则图中阴影部分的面积$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$.
如图,正方形ABCD的边长为1,分别以A、D为圆心,1为半径画弧BD、AC,则图中阴影部分的面积$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$. 如图,BD是△ABC的中线,AB=6cm,BC=4cm,则△ABD和△BCD的周长差为2cm.
如图,BD是△ABC的中线,AB=6cm,BC=4cm,则△ABD和△BCD的周长差为2cm.