题目内容
1.已知反比例函数y=$\frac{2k-1}{x}$的图象在每个象限内函数值y随自变量x增大而减小,且k的值还满足9-2(2k-1)≥2k-1,若k为整数,求反比例函数的解析式.分析 根据反比例函数的性质可得2k-1>0,解得k>$\frac{1}{2}$,解不等式9-2(2k-1)≥2k-1得k≤2,进而可得k的取值范围,然后再确定k的值,进而可得反比例函数解析式.
解答 解:∵反比例函数y=$\frac{2k-1}{x}$的图象在每个象限内函数值y随自变量x增大而减小,
∴2k-1>0,
解得:k>$\frac{1}{2}$,
9-2(2k-1)≥2k-1,
解得:k≤2,
∴$\frac{1}{2}<$k≤2,
∵k为整数,
∴k=1,2,
∴反比函数的解析式为y=$\frac{1}{x}$或y=$\frac{3}{x}$.
点评 此题主要考查了反比例函数的性质,以及待定系数法求反比例函数解析式,关键是正确确定k的取值范围.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
11.在△ABC中,∠ACB=90°,AC=1,BC=2,则下列说法正确的是( )
| A. | ∠B=30° | B. | 斜边上的中线长为1 | ||
| C. | 该三角形外接圆的半径为1 | D. | 斜边上高线长为$\frac{2}{5}\sqrt{5}$ |
16.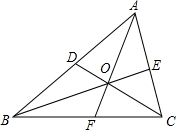 如图,在△ABC中,∠BAC、∠ABC的平分线AF、BE交于点O,连接CD并延长交AB边于点D,则CD是△ABC的( )
如图,在△ABC中,∠BAC、∠ABC的平分线AF、BE交于点O,连接CD并延长交AB边于点D,则CD是△ABC的( )
 如图,在△ABC中,∠BAC、∠ABC的平分线AF、BE交于点O,连接CD并延长交AB边于点D,则CD是△ABC的( )
如图,在△ABC中,∠BAC、∠ABC的平分线AF、BE交于点O,连接CD并延长交AB边于点D,则CD是△ABC的( )| A. | 角平分线 | B. | 中线 | C. | 高 | D. | 以上都不对 |
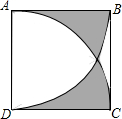 如图,正方形ABCD的边长为1,分别以A、D为圆心,1为半径画弧BD、AC,则图中阴影部分的面积$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$.
如图,正方形ABCD的边长为1,分别以A、D为圆心,1为半径画弧BD、AC,则图中阴影部分的面积$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$. 如图,BD是△ABC的中线,AB=6cm,BC=4cm,则△ABD和△BCD的周长差为2cm.
如图,BD是△ABC的中线,AB=6cm,BC=4cm,则△ABD和△BCD的周长差为2cm. 如图,在四边形ABCD中,∠BAD=90°,∠CBD=90°,且AD=4,AB=3,BC=12.求正方形DCEF的面积.
如图,在四边形ABCD中,∠BAD=90°,∠CBD=90°,且AD=4,AB=3,BC=12.求正方形DCEF的面积.