题目内容
7.先化简$\frac{2a+4}{a-2}$÷(a+2)+$\frac{{a}^{2}-4}{{a}^{2}-4a+4}$,再求值,a为整数且-2≤a≤2.分析 先根据分式混合运算的法则把原式进行化简,再求出a的值代入进行计算即可.
解答 解:原式=$\frac{2(a+2)}{a-2}$•$\frac{1}{a+2}$+$\frac{(a+2)(a-2)}{(a-2)^{2}}$
=$\frac{2}{a-2}$+$\frac{a+2}{a-2}$
=$\frac{a+4}{a-2}$,
∵a为整数且-2≤a≤2且a≠±2,
∴当a=1时,原式=-5;
当a=-1时,原式=-1;
当a=0时,原式=-2.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
18.若m2-m-1=0,则代数式m2-m+2013的值为( )
| A. | 2011 | B. | 2012 | C. | 2013 | D. | 2014 |
15.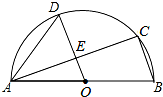 如图,AB是半圆O的直径,C、D是半圆O上的两点,OD∥BC,OD与AC交于点E.下列结论不一定成立的是( )
如图,AB是半圆O的直径,C、D是半圆O上的两点,OD∥BC,OD与AC交于点E.下列结论不一定成立的是( )
 如图,AB是半圆O的直径,C、D是半圆O上的两点,OD∥BC,OD与AC交于点E.下列结论不一定成立的是( )
如图,AB是半圆O的直径,C、D是半圆O上的两点,OD∥BC,OD与AC交于点E.下列结论不一定成立的是( )| A. | △AOD是等边三角形 | B. | $\widehat{AD}$=$\widehat{CD}$ | ||
| C. | ∠ACB=90° | D. | OE=$\frac{1}{2}$BC |
19.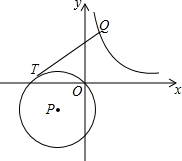 如图,在平面直角坐标系中,⊙P的圆心坐标是(-1,-1),半径为$\sqrt{2}$,点Q是函数y=$\frac{1}{x}$的图象上一动点,过点Q作⊙P的切线QT,切点为T,则线段QT长度的最小值为( )
如图,在平面直角坐标系中,⊙P的圆心坐标是(-1,-1),半径为$\sqrt{2}$,点Q是函数y=$\frac{1}{x}$的图象上一动点,过点Q作⊙P的切线QT,切点为T,则线段QT长度的最小值为( )
 如图,在平面直角坐标系中,⊙P的圆心坐标是(-1,-1),半径为$\sqrt{2}$,点Q是函数y=$\frac{1}{x}$的图象上一动点,过点Q作⊙P的切线QT,切点为T,则线段QT长度的最小值为( )
如图,在平面直角坐标系中,⊙P的圆心坐标是(-1,-1),半径为$\sqrt{2}$,点Q是函数y=$\frac{1}{x}$的图象上一动点,过点Q作⊙P的切线QT,切点为T,则线段QT长度的最小值为( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{6}$ | D. | 4 |
16.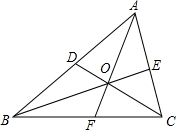 如图,在△ABC中,∠BAC、∠ABC的平分线AF、BE交于点O,连接CD并延长交AB边于点D,则CD是△ABC的( )
如图,在△ABC中,∠BAC、∠ABC的平分线AF、BE交于点O,连接CD并延长交AB边于点D,则CD是△ABC的( )
 如图,在△ABC中,∠BAC、∠ABC的平分线AF、BE交于点O,连接CD并延长交AB边于点D,则CD是△ABC的( )
如图,在△ABC中,∠BAC、∠ABC的平分线AF、BE交于点O,连接CD并延长交AB边于点D,则CD是△ABC的( )| A. | 角平分线 | B. | 中线 | C. | 高 | D. | 以上都不对 |
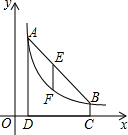 如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.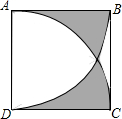 如图,正方形ABCD的边长为1,分别以A、D为圆心,1为半径画弧BD、AC,则图中阴影部分的面积$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$.
如图,正方形ABCD的边长为1,分别以A、D为圆心,1为半径画弧BD、AC,则图中阴影部分的面积$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$.