题目内容
11.△ABC的三边长为a,b,c,其中a和b满足b2-4b+4+$\sqrt{a-5}$=0,求c的取值范围.分析 首先分解因式,根据非负数的性质求出a,b的值,然后根据三角形三边关系定理:三角形两边之和大于第三边,三角形的两边差小于第三边即可求出c的取值范围.
解答 解:∵b2-4b+4+$\sqrt{a-5}$=(b-2)2+$\sqrt{a-5}$=0,
∴b-2=0,a-5=0,
解得:a=5,b=2,
∴5-2<c<5+2,
即3<c<7.
点评 此题主要考查了配方法的运用,三角形的三边关系,以及非负数的性质,关键是求出a,b的值,熟练掌握三角形的三边关系.

练习册系列答案
相关题目
1.下列二次根式是最简二次根式的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{14}$ | C. | $\sqrt{16}$ | D. | $\sqrt{18}$ |
19.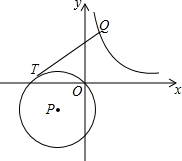 如图,在平面直角坐标系中,⊙P的圆心坐标是(-1,-1),半径为$\sqrt{2}$,点Q是函数y=$\frac{1}{x}$的图象上一动点,过点Q作⊙P的切线QT,切点为T,则线段QT长度的最小值为( )
如图,在平面直角坐标系中,⊙P的圆心坐标是(-1,-1),半径为$\sqrt{2}$,点Q是函数y=$\frac{1}{x}$的图象上一动点,过点Q作⊙P的切线QT,切点为T,则线段QT长度的最小值为( )
 如图,在平面直角坐标系中,⊙P的圆心坐标是(-1,-1),半径为$\sqrt{2}$,点Q是函数y=$\frac{1}{x}$的图象上一动点,过点Q作⊙P的切线QT,切点为T,则线段QT长度的最小值为( )
如图,在平面直角坐标系中,⊙P的圆心坐标是(-1,-1),半径为$\sqrt{2}$,点Q是函数y=$\frac{1}{x}$的图象上一动点,过点Q作⊙P的切线QT,切点为T,则线段QT长度的最小值为( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{6}$ | D. | 4 |
16.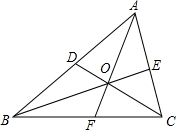 如图,在△ABC中,∠BAC、∠ABC的平分线AF、BE交于点O,连接CD并延长交AB边于点D,则CD是△ABC的( )
如图,在△ABC中,∠BAC、∠ABC的平分线AF、BE交于点O,连接CD并延长交AB边于点D,则CD是△ABC的( )
 如图,在△ABC中,∠BAC、∠ABC的平分线AF、BE交于点O,连接CD并延长交AB边于点D,则CD是△ABC的( )
如图,在△ABC中,∠BAC、∠ABC的平分线AF、BE交于点O,连接CD并延长交AB边于点D,则CD是△ABC的( )| A. | 角平分线 | B. | 中线 | C. | 高 | D. | 以上都不对 |
1.若$\sqrt{{a}^{2}}$=-a,则正确的是( )
| A. | a>0 | B. | a≥0 | C. | a<0 | D. | a≤0 |
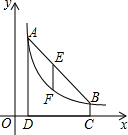 如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.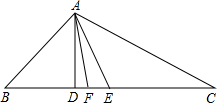 如图,完成下面几何语言的表达.
如图,完成下面几何语言的表达.