题目内容
8．方程x2+16=8x的根的情况为（ ）| A． | 有两个不相等的实数根 | B． | 有两个相等的实数根 | ||
| C． | 有一个实数根 | D． | 没有实数根 |
分析 方程整理为x2-8x+16=0，把a=1，b=-8，c=16代入△=b2-4ac进行计算，然后根据计算结果判断方程根的情况．
解答 解：方程整理为x2-8x+16=0，
∵a=1，b=-8，c=16，
∴△=b2-4ac=（-8）2-4×1×16=0，
所以方程有两个相等的实数根．
故选：B．
点评 本题考查了一元二次方程ax2+bx+c=0（a≠0，a，b，c为常数）的根的判别式△=b2-4ac．当△＞0时，方程有两个不相等的实数根；当△=0时，方程有两个相等的实数根；当△＜0时，方程没有实数根．
练习册系列答案
相关题目
18．若m2-m-1=0，则代数式m2-m+2013的值为（ ）
| A． | 2011 | B． | 2012 | C． | 2013 | D． | 2014 |
19．
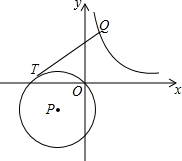如图，在平面直角坐标系中，⊙P的圆心坐标是（-1，-1），半径为$\sqrt{2}$，点Q是函数y=$\frac{1}{x}$的图象上一动点，过点Q作⊙P的切线QT，切点为T，则线段QT长度的最小值为（ ）
如图，在平面直角坐标系中，⊙P的圆心坐标是（-1，-1），半径为$\sqrt{2}$，点Q是函数y=$\frac{1}{x}$的图象上一动点，过点Q作⊙P的切线QT，切点为T，则线段QT长度的最小值为（ ）| A． | 2$\sqrt{2}$ | B． | 2$\sqrt{3}$ | C． | $\sqrt{6}$ | D． | 4 |
16．
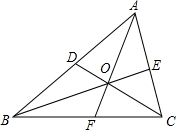如图，在△ABC中，∠BAC、∠ABC的平分线AF、BE交于点O，连接CD并延长交AB边于点D，则CD是△ABC的（ ）
如图，在△ABC中，∠BAC、∠ABC的平分线AF、BE交于点O，连接CD并延长交AB边于点D，则CD是△ABC的（ ）| A． | 角平分线 | B． | 中线 | C． | 高 | D． | 以上都不对 |
如图，BD是△ABC的中线，AB=6cm，BC=4cm，则△ABD和△BCD的周长差为2cm．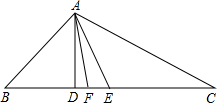
如图，完成下面几何语言的表达．
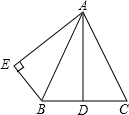如图，AB=AC，点D是BC的中点，AB平分∠DAE，AE⊥BE，垂足为E．那么AD与AE有什么关系？请说明理由．