题目内容
3.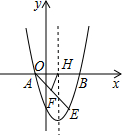 如图,抛物线y=x2+bx+c经过点A(-1,0),B(3,0).
如图,抛物线y=x2+bx+c经过点A(-1,0),B(3,0).(1)求抛物线的解析式;
(2)点E(2,m)在抛物线上,抛物线的对称轴与x轴交于点H,点F是AE中点,连接FH,求线段FH的长;
(3)P为AE下方抛物线上的点,当△AEP的面积最大时,求P点的坐标.
分析 (1)由于抛物线y=x2+bx+c经过A(-1,0),B(3,0)两点,根据待定系数法可求抛物线的解析式;
(2)先得到点E(2,-3),根据勾股定理可求BE,再根据直角三角形的性质可求线段HF的长;
(3)先确定出直线AE解析式,设出点P的坐标,进而表示出点G的坐标,用三角形的面积的计算方法建立函数关系式,即可确定出最大值.
解答 解:(1)∵抛物线y=x2+bx+c经过点A(-1,0),B(3,0),
∴$\left\{\begin{array}{l}{1-b+c=0}\\{9+3b+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=-2}\\{c=-2}\end{array}\right.$.
∴抛物线的解析式为:y=x2-2x-3;
(2)∵点E(2,m)在抛物线上,
∴m=4-4-3=-3,
∴E(2,-3),
∴BE=$\sqrt{(3-2)^{2}+(0+3)^{2}}$=$\sqrt{10}$,
∵点F是AE中点,抛物线的对称轴与x轴交于点H,即H为AB的中点,
∴FH是三角形ABE的中位线,
∴FH=$\frac{1}{2}$BE=$\frac{1}{2}$×$\sqrt{10}$=$\frac{\sqrt{10}}{2}$;
(3)如图,
过点P作PG∥y轴交AE于G,连接AP,PE,
由(2)知,E(2,-3),
∵A(-1,0),
∴直线OE的解析式为y=-x-1
设P(n,n2-2n-3),(-1<n<2)
∴G(n,-n-1),
∴PG=-n-1-(n2-2n-3)=-n2+n+2,
∴S△APE=S△APG+S△EPG
=$\frac{1}{2}$PG•|xP-xA|+$\frac{1}{2}$PG•|xE-xP|
=$\frac{1}{2}$PG(xP-xA+xE-xP)
=$\frac{1}{2}$PG×(xE-xA)
=$\frac{1}{2}$(-n2+n+2)(2+1)
=-$\frac{3}{2}$(n2-n-2)
=-$\frac{3}{2}$(n-$\frac{1}{2}$)2+$\frac{27}{8}$,
∴当n=$\frac{1}{2}$时,S△APE=$\frac{27}{8}$,此时,P($\frac{1}{2}$,-$\frac{15}{4}$).
点评 此题考查了二次函数综合题,涉及的知识点有:待定系数法求抛物线的解析式,勾股定理,直角三角形的性质,三角形面积的计算,方程思想的应用,综合性较强,有一定的难度.

 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案| A. | k<9且k≠0 | B. | k<9 | C. | k≤9且k≠0 | D. | k≥9 |
 某台阶如图,现要在台阶上铺地毯,那么至少需要地毯4.1米.
某台阶如图,现要在台阶上铺地毯,那么至少需要地毯4.1米.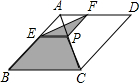 如图所示,菱形ABCD的对角线的长分别为4和6,P是对角线AC上任一点(点P不与点A、C重合),且PE∥BC交AB于E,PF∥CD交AD于F,则阴影部分的面积是6.
如图所示,菱形ABCD的对角线的长分别为4和6,P是对角线AC上任一点(点P不与点A、C重合),且PE∥BC交AB于E,PF∥CD交AD于F,则阴影部分的面积是6.
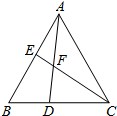 如图,在△ABC中,∠BAC=∠B=60°,AB=AC,点D、E分别是边BC、AB所在直线上的动点,且BD=AE,AD与CE交于点F.当点D、E在边BC、AB上运动时,求∠DFC的度数.
如图,在△ABC中,∠BAC=∠B=60°,AB=AC,点D、E分别是边BC、AB所在直线上的动点,且BD=AE,AD与CE交于点F.当点D、E在边BC、AB上运动时,求∠DFC的度数.